 KeePass
KeePass- 关注
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
 本文由
KeePass 创作,已纳入「FreeBuf原创奖励计划」,未授权禁止转载
本文由
KeePass 创作,已纳入「FreeBuf原创奖励计划」,未授权禁止转载
日期:2021-08-30
作者:Jgk01
介绍:常见
CTF中RSA题目的总结与解题方法,参考了一些平台的题目和文章进行总结。
0x00 前言
整篇RSA密码学题目总结文章给看官老爷们下个菜。
0x01 RSA简单题目
1.1 VeryEasyRSA
题目要求:已知RSA公钥生成参数:
p = 3487583947589437589237958723892346254777
q = 8767867843568934765983476584376578389
e = 65537
求d = ?
最简单的题型,使用gmpy2库或者libnum库都有函数解密,解题脚本如下(两个都行):
import gmpy2
p = 3487583947589437589237958723892346254777
q = 8767867843568934765983476584376578389
e = 65537
phi = (p-1)*(q-1)
d = libnum.invert(e,phi)
print d
import libnum
p = 3487583947589437589237958723892346254777
q = 8767867843568934765983476584376578389
e = 65537
phi = (p-1)*(q-1)
d = libnum.invmod(e,phi)
print d
都可以求出d来。
1.2 easyRSA
题目信息:
已知一段RSA加密的信息为:0xdc2eeeb2782c且已知加密所用的公钥:(N=322831561921859 e = 23)
请解密出明文,提交时请将数字转化为ascii码提交
比如你解出的明文是0x6162,那么请提交字符串ab
提交格式:PCTF{明文字符串}
这个就是典型的发给你密文求明文,给了n你需要去分解成p,q一般只需要在线网站分解就行,kali有个工具叫factor,用这个也行。在线网站的话:factored.com解题脚本如下。
#!/usr/bin/python
#coding:utf-8
import libnum
from Crypto.Util.number import long_to_bytes
c = 0xdc2eeeb2782c
n = 322831561921859
e = 23
q = 13574881
p = 23781539
d = libnum.invmod(e, (p - 1) * (q - 1))
m = pow(c, d, n)
print "m的值为:"
print long_to_bytes(m)
1.3 MediumRSA
这是RSA常见的入门题目,算是解密题了,题目给了两个文件

这里flag.enc是密文,而pubkey.pem是公钥,正常的话是需要私钥才能解出密码,这里我们就需要利用公钥来获取信息了
openssl rsa -pubin -in pubkey.pem -text -modulus
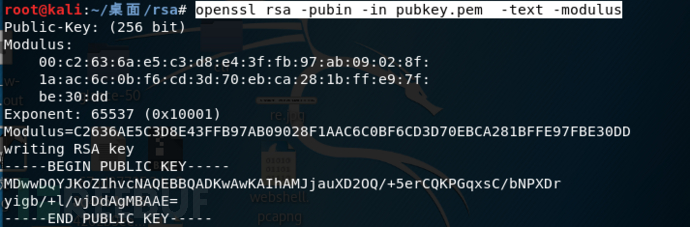
通过读取公钥中的信息,我们可以知道Expoent:65537是e,下面的Modulus是16进制的n,把它转换为十进制就是n

p=275127860351348928173285174381581152299
q=319576316814478949870590164193048041239
现在就有了n,p,q,e,c,所以可以根据p,q求出phi((p-1)(q-1)),再根据c,d,n,即可求出明文m,解题脚本如下。
import libnum
from Crypto.Util.number import long_to_bytes
n=87924348264132406875276140514499937145050893665602592992418171647042491658461
p = 275127860351348928173285174381581152299
q = 319576316814478949870590164193048041239
e = 65537
phi = (p-1)*(q-1)
d = libnum.invmod(e,phi)
c = int('6D3EB7DF23EEE1D38710BEBA78A0878E0E9C65BD3D08496DDA64924199110C79',16)
m = pow(c,d,n)
print long_to_bytes(m)
这里c就是flag.enc这个文件的16进制打开,然后把它转成10进制。
0x02 RSA基础题目
2.1 babyRSA
这是一个还算有意思的题,题目给的已知条件如下:
p+q:0x1232fecb92adead91613e7d9ae5e36fe6bb765317d6ed38ad890b4073539a6231a6620584cea5730b5af83a3e80cf30141282c97be4400e33307573af6b25e2ea
(p+1)(q+1) : 0x5248becef1d925d45705a7302700d6a0ffe5877fddf9451a9c1181c4d82365806085fd86fbaab08b6fc66a967b2566d743c626547203b34ea3fdb1bc06dd3bb765fd8b919e3bd2cb15bc175c9498f9d9a0e216c2dde64d81255fa4c05a1ee619fc1fc505285a239e7bc655ec6605d9693078b800ee80931a7a0c84f33c851740
e : 0xe6b1bee47bd63f615c7d0a43c529d219
d : 0x2dde7fbaed477f6d62838d55b0d0964868cf6efb2c282a5f13e6008ce7317a24cb57aec49ef0d738919f47cdcd9677cd52ac2293ec5938aa198f962678b5cd0da344453f521a69b2ac03647cdd8339f4e38cec452d54e60698833d67f9315c02ddaa4c79ebaa902c605d7bda32ce970541b2d9a17d62b52df813b2fb0c5ab1a5
enc_flag : 0x50ae00623211ba6089ddfae21e204ab616f6c9d294e913550af3d66e85d0c0693ed53ed55c46d8cca1d7c2ad44839030df26b70f22a8567171a759b76fe5f07b3c5a6ec89117ed0a36c0950956b9cde880c575737f779143f921d745ac3bb0e379c05d9a3cc6bf0bea8aa91e4d5e752c7eb46b2e023edbc07d24a7c460a34a9a
这里我们需要动一下小脑袋,我们发现这里没有n,没有给p,q这咋办呢?这时候我们看到题目给了p+q还给了(p+1)(q+1),这时候我们就应该发现问题了(p+1)(q+1)=pq+q+p+1=n+(p+q)+1
这里(p+1)(q+1)是已知的,我们用y来代替y=(p+q+1)+n
设x=p+q+1,n=y-x,phi=(p-1)(q-1)=n-(p+q)=1=n-x+2。
解题脚本如下。
import libnum
from Crypto.Util.number import long_to_bytes
x = 0x1232fecb92adead91613e7d9ae5e36fe6bb765317d6ed38ad890b4073539a6231a6620584cea5730b5af83a3e80cf30141282c97be4400e33307573af6b25e2ea + 1
y = 0x5248becef1d925d45705a7302700d6a0ffe5877fddf9451a9c1181c4d82365806085fd86fbaab08b6fc66a967b2566d743c626547203b34ea3fdb1bc06dd3bb765fd8b919e3bd2cb15bc175c9498f9d9a0e216c2dde64d81255fa4c05a1ee619fc1fc505285a239e7bc655ec6605d9693078b800ee80931a7a0c84f33c851740
c = 0x50ae00623211ba6089ddfae21e204ab616f6c9d294e913550af3d66e85d0c0693ed53ed55c46d8cca1d7c2ad44839030df26b70f22a8567171a759b76fe5f07b3c5a6ec89117ed0a36c0950956b9cde880c575737f779143f921d745ac3bb0e379c05d9a3cc6bf0bea8aa91e4d5e752c7eb46b2e023edbc07d24a7c460a34a9a
e = 0xe6b1bee47bd63f615c7d0a43c529d219
n = y-x
phi = n-x+2
d = libnum.invmod(e,phi)
m = pow(c,d,n)
print long_to_bytes(m)
2.2 e=2把c开方求解
题目要求:
e=2
c=9217979941366220275377875095861710925207028551771520610387238734819759256223080175603032167658086669886661302962985046348865181740591251321966682848536331583243529
求明文m。RSA加密,由于e只有2,相当于把明文m平方而已,得到的c也比n小很多。
尝试把c开根号看能否得到明文。
一般的python开根号方法精度较低,对大整数开出来的根号准确度低可以使用gmpy2库对大整数开根号。解题脚本如下。
#!/usr/bin/python
#coding:utf-8
import gmpy2
import libnum
import codecs,binascii
c = 9217979941366220275377875095861710925207028551771520610387238734819759256223080175603032167658086669886661302962985046348865181740591251321966682848536331583243529
m = gmpy2.isqrt(c)
m = int(m)
def sss(n):
s = hex(n)[2:-1]
if len(s) % 2 != 0:
s = "0x" + s
return str(codecs.decode(s, 'hex'))
print sss(m)
2.3 Rabin加密中的N可被分解
适用情况:e==2Rabin加密是RSA的衍生算法,e==2是Rabin加密典型特征,可以百度或阅读https://en.维基pedia.org/wiki/Rabin_cryptosystem以了解到详细的说明,
这里只关注解密方法。一般先通过其他方法分解得到p,q,然后解密。解题脚本如下。

#!/usr/bin/python
#coding:utf-8
import codecs,binascii
import gmpy2,libnum
n=87924348264132406875276140514499937145050893665602592992418171647042491658461
p=275127860351348928173285174381581152299
q=319576316814478949870590164193048041239
e=2
c=int('39DE036DE3132757E819F769EAD64BB487EE3F47E67843AFB73748FD9E979BE0',16)
mp=pow(c,(p+1)/4,p)
mq=pow(c,(q+1)/4,q)
yp=gmpy2.invert(p,q)
yq=gmpy2.invert(q,p)
r=(yp*p*mq+yq*q*mp)%n
rr=n-r
s=(yp*p*mq-yq*q*mp)%n
ss=n-s
def sss(n):
s = hex(n)[2:]
if len(s) % 2 != 0:
s = "0" + s
return str(codecs.decode(s, 'hex'))
print sss(ss)
2.4 e=3小明文攻击
适用情况:e较小,一般为3。
公钥e很小,明文m也不大的话,于是m^e=k*n+m中的的k值很小甚至为0,爆破k或直接开三次方即可。解题脚本如下。
#!/usr/bin/python
#coding:utf-8
import codecs
import gmpy2,binascii,libnum,time
n=0xB0BEE5E3E9E5A7E8D00B493355C618FC8C7D7D03B82E409951C182F398DEE3104580E7BA70D383AE5311475656E8A964D380CB157F48C951ADFA65DB0B122CA40E42FA709189B719A4F0D746E2F6069BAF11CEBD650F14B93C977352FD13B1EEA6D6E1DA775502ABFF89D3A8B3615FD0DB49B88A976BC20568489284E181F6F11E270891C8EF80017BAD238E363039A458470F1749101BC29949D3A4F4038D463938851579C7525A69984F15B5667F34209B70EB261136947FA123E549DFFF00601883AFD936FE411E006E4E93D1A00B0FEA541BBFC8C5186CB6220503A94B2413110D640C77EA54BA3220FC8F4CC6CE77151E29B3E06578C478BD1BEBE04589EF9A197F6F806DB8B3ECD826CAD24F5324CCDEC6E8FEAD2C2150068602C8DCDC59402CCAC9424B790048CCDD9327068095EFA010B7F196C74BA8C37B128F9E1411751633F78B7B9E56F71F77A1B4DAAD3FC54B5E7EF935D9A72FB176759765522B4BBC02E314D5C06B64D5054B7B096C601236E6CCF45B5E611C805D335DBAB0C35D226CC208D8CE4736BA39A0354426FAE006C7FE52D5267DCFB9C3884F51FDDFDF4A9794BCFE0E1557113749E6C8EF421DBA263AFF68739CE00ED80FD0022EF92D3488F76DEB62BDEF7BEA6026F22A1D25AA2A92D124414A8021FE0C174B9803E6BB5FAD75E186A946A17280770F1243F4387446CCCEB2222A965CC30B3929
e=3
res=0
c=int('85C0DE5F89E88720AFD485F91DED38E9EAEDA3A61DDEE7087BBD29920EE40B6D53565EDD1E418095586BD4F33015729D433AF413C660E4C0B164ED025F91216D904578F7F20C5FB1E09E71992198D8E8D7FBD917597AEE45EBF4CA80124CE9B47ED163F0B9D5716A9D6E1F5B8AE09B16CAE30BBD64A15E17CC39A90FB62536AD943CDDA9A4AAC5978E3C93502535D5353638BC708C9B59CC9DC7BCB1D873336CE081591522B1D48904463783DD6837B1C41B8011889648E0ACDFBD3EE259F717990828D16DB34EB982446216DB534DC06B9E7AAF90BCCB54A1CC77C2813BDFE9A1B5C2E958C3EA8CA103BA1A89036B7014BBC962EB7A8C910E095BB83791BD9FEEE0D8F6AF0C2E030CCCC6D8729743419BDEE0A1E45AB5E7324A344761C8CC8DB30961A971D566E49C4562924C3EE001EDECE3445CD28DBA264BA8A90C5E533542096C26AA7D874997A308025A5E95BFC6949EBD16CEA889D242AB2E2FF2446090D07666D7574946E391D3F153D50346BC75DA94634182DF80F7BA97B77AF8922F13E43B2DF788902A209B9E569DD3C6FAA4DD7B43899F59798845DF642EDEEF34A186949CBE83C099F085F87A299591E715CCB4FE74612B00AEBE25C114819CF887C256121915416ACBCB058937E3D39EB7EF7143E145131119DA9C3D9818599A0E5109727FB581BBC20EB3E6A25011B8E9034537C0E580A0EE8F1553805BE8',16)
print time.asctime()
def sss(n):
s = hex(n)[2:]
if len(s) % 2 != 0:
s = "0" + s
return str(codecs.decode(s, 'hex'))
for i in xrange(200000000):
if gmpy2.iroot(c+n*i,3)[1]==1:
res=gmpy2.iroot(c+n*i,3)[0]
print i,res
print sss(res)
print time.asctime()
break
2.5 Roll按行加密
题目文件{920139713,19}
704796792
752211152
274704164
18414022
368270835
483295235
263072905
459788476
483295235
459788476
663551792
475206804
459788476
428313374
475206804
459788476
425392137
704796792
458265677
341524652
483295235
534149509
425392137
428313374
425392137
341524652
458265677
263072905
483295235
828509797
341524652
425392137
475206804
428313374
483295235
475206804
459788476
306220148
不要总是觉得c就是一连串的字符串,也可以是分行的,记住不要分行符删除把c变为一个字符串。
应该按行进行解密
根据给出的文件应该是:n为920139713e为19
因此解题脚本如下。
#!/usr/bin/python
#coding:utf-8
import gmpy2
from Crypto.Util.number import long_to_bytes
n = 920139713
p = 49891
q = 18443
e = 19
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)
m = ""
with open('roll.txt','r') as f:
for c in f.readlines():
m += long_to_bytes(pow(int(c), d, n))
print m
2.6 模不互素
这个题目就是两个n然后共用一个e,之后是两个密文
适用情况:存在两个或更多模数 ,且gcd(N1,N2)!=1。
多个模数n共用质数,则可以很容易利用欧几里得算法求得他们的质因数之一gcd(N1,N2),然后这个最大公约数可用于分解模数分别得到对应的p和q,即可进行解密,解题脚本如下。
#!/usr/bin/python
#coding:utf-8
import gmpy2
from Crypto.Util.number import long_to_bytes
c1 = 0x8BD7BF995BF9E16A0D04ADB49A2411C74FFDB0DB4F35DB3A79A1B44691947C9824085BC4CA5F7F4EFA3C8FD0BC3E870AA6D5E15307A63A2172C44C5903D35785B8D06B51651EE7106B070D5A6AABA089AB67609661265B74914C865F863DC1D2DC08CE0B026107A74EC3FDC62666B50110B9D15A243EAAD6F53646929A3369285404868E42DD0BBE92D956018E3C0B36EF5E9516E433228CFDD06D6E662EC0A9A31061EA11F61CA17EABF43D2D4977FC9D6FC53AB6DC01509401B8D9A46B59A9ADAA97D54CC50C27445E4C21B893510620EC3566AD6E8727FA147437B207505217E6F2DF009E2286C8354D281374D7802D08A2062FE48DBF135BBCAB120EBF84
c2 = 0x8C3CF3161AA3E37831030985C60566A7604688B73E5B1D3B36E72EF06ED4F71289EFE80E0D94BD755034E6C210F17DA85B9D0388F3AD104C68BC514A8EB1569A109EB5F266F7C5FA4DDFA638258949B43D4CF1406720CCD4CA11E74FDF8AEB35C56A79781C87157FC4213573329C5B0FF411F8A4F34580AA103DB9FD403C0D409FA11860A7C4595FDC49DC2CF94E5112B772E5DEC8F17E24B10A7FD7A95DCB87BE5E27C32FC931574A7847BC506A61EFE9DB3D3F612143845FE80D7B3EA548B886A67A29CBDB2775B1F91178B6DA763F1A6ECFF46592E4C7FFAAB6C9FEF29D9CB9E035A3D98ECFFB26BA2EEAA56D1CD096E6A2CF9A58086CAD7718DDA5CB0C1B
n1 = 18674375108313094928585156581138941368570022222190945461284402673204018075354069827186085851309806592398721628845336840532779579197302984987661547245423180760958022898546496524249201679543421158842103496452861932183144343315925106154322066796612415616342291023962127055311307613898583850177922930685155351380500587263611591893137588708003711296496548004793832636078992866149115453883484010146248683416979269684197112659302912316105354447631916609587360103908746719586185593386794532066034112164661723748874045470225129298518385683561122623859924435600673501186244422907402943929464694448652074412105888867178867357727
n2 = 20071978783607427283823783012022286910630968751671103864055982304683197064862908267206049336732205051588820325894943126769930029619538705149178241710069113634567118672515743206769333625177879492557703359178528342489585156713623530654319500738508146831223487732824835005697932704427046675392714922683584376449203594641540794557871881581407228096642417744611261557101573050163285919971711214856243031354845945564837109657494523902296444463748723639109612438012590084771865377795409000586992732971594598355272609789079147061852664472115395344504822644651957496307894998467309347038349470471900776050769578152203349128951
p1 = gmpy2.gcd(n1, n2)
assert (p1 != 1)
p2 = n1 / p1
p3 = n2 / p1
e = 0x10001
d1 = gmpy2.invert(e, (p1 - 1) * (p2 - 1))
d2 = gmpy2.invert(e, (p1 - 1) * (p3 - 1))
m1 = pow(c1, d1, n1)
m2 = pow(c2, d2, n2)
print long_to_bytes(m1)+long_to_bytes(m2)
2.7 共模攻击
一个n两个e,两个密文,然后e1与e2互质适用情况
明文m、模数n相同,公钥指数e、密文c不同,gcd(e1,e2)==1
对同一明文的多次加密使用相同的模数和不同的公钥指数可能导致共模攻击,题目内容及解题脚本如下。
#!/usr/bin/python
#coding:utf-8
import re
import gmpy2
from Crypto.Util.number import long_to_bytes
e1 = 17
e2 = 65537
n = 0x00b0bee5e3e9e5a7e8d00b493355c618fc8c7d7d03b82e409951c182f398dee3104580e7ba70d383ae5311475656e8a964d380cb157f48c951adfa65db0b122ca40e42fa709189b719a4f0d746e2f6069baf11cebd650f14b93c977352fd13b1eea6d6e1da775502abff89d3a8b3615fd0db49b88a976bc20568489284e181f6f11e270891c8ef80017bad238e363039a458470f1749101bc29949d3a4f4038d463938851579c7525a69984f15b5667f34209b70eb261136947fa123e549dfff00601883afd936fe411e006e4e93d1a00b0fea541bbfc8c5186cb6220503a94b2413110d640c77ea54ba3220fc8f4cc6ce77151e29b3e06578c478bd1bebe04589ef9a197f6f806db8b3ecd826cad24f5324ccdec6e8fead2c2150068602c8dcdc59402ccac9424b790048ccdd9327068095efa010b7f196c74ba8c37b128f9e1411751633f78b7b9e56f71f77a1b4daad3fc54b5e7ef935d9a72fb176759765522b4bbc02e314d5c06b64d5054b7b096c601236e6ccf45b5e611c805d335dbab0c35d226cc208d8ce4736ba39a0354426fae006c7fe52d5267dcfb9c3884f51fddfdf4a9794bcfe0e1557113749e6c8ef421dba263aff68739ce00ed80fd0022ef92d3488f76deb62bdef7bea6026f22a1d25aa2a92d124414a8021fe0c174b9803e6bb5fad75e186a946a17280770f1243f4387446ccceb2222a965cc30b3929L
c1=int('71B38B33CAD0F3BF34D726ACAC37836EC15B159FB701E7A62B7D2ACE5E05F3F8A3C32458D69EE7AB04C22B4CAE0866B964C21649EBB6B957D0AEEAFACF9D6AFCDF8DF1C8648BF39EB7529E1CC05BE90EA4D9BF14CAE81F63842598907575E444EC3F70EFACC09F9D701481D9DB0DDE722F49C2959B087F37012FED3F99391DB733695EF4E5102E724A40EAC0DC1470D923B58641D1F7DDB1186C98AA157F116BBB52FD3F343935F2E47EA5A58609068CBE33B1B95AECC745A4820CCE678A2B36AA039A9325CF96945BC6F169591CFF6F3A54BEC8DF1B341729DA9489BC7695F3DAF41A4888C7AB9FAE7A753A78F7891522CC952B880FED4D1C400424F312F4801CFEF4A7EBAF3ABF5E2FB24BE69BED6903694C3BA5AA4B81E06400A2FBB2D2F9538325176ED10F17B7B2F1A3C5D85357126781CB979484A93ACF2C5D20DA22055A4FFC8E174363046D91E01FCB5C7B4C3844C1494A2D964E669D59EB2A6ECD18F75914DE748CA182233C8D6A4DA7C7E7611A2FB5A9C0BA26B28E6F5EAEADDA4BB2CC5F41A716C6D1043662B5F45305EBECA853A3035347D65961B3D083752D692CB6F148BF69EEAA4AF586A7FD909073377C5124E51A6D8E38840594EF5AE3F6497A2A9EC06ACC63E665C96E76801E9A271C597E2637018AA341EF9F321B9BF81EC84344FBCB040BB705D4B713FE6007E30A8816EEAE561110B95CDA1CA64181',16)
c2=int('30068A183D1635C7B06C07DA18A0A39A33298C734E3EDB6C55A83DD23B620CD052AD5DC0190C5C998D76093D363210198D55902F285F74D4B0EECC6E296A86EF3D4F2525A5128E9C1A0D07A610C65275D5D05DCEBE3AA198911F1ED33361185B2CD7B6ABAA2ACA512994F34CF029AF91BEA7F64D4869D42C90AD983C24D67870E5A45ED37F45FC4DC24645752F384E928654127D1F1F838831A42DC4DF76AF88A88BACB6945B22C46764C031D332FEA23D8FD9ADBBBA2394759EF4FDBEFC60A277C465FC1190BFD295F756FF8C096B6F3518B6B73A7BDC02A12B8A43BBA58948D3ED62815BF1C5E51D51B8223F1532ECD426DFC769BCDB207386FE2D8515F1ADB355FE0FA96D06856973C80BD3C08CF3779391E7B07A31616DE53009E9BDBD67693AE1599F6B4BAEDF370C451F2D5C7F6782A92BF910524AB5445120E7CD717331CE33253630C3DCA3BBA9308BA1546B477CFAB17103BA4350E5A40F2812FD3F303B5218C9CA25CE64AA51E7F2D026AC82784F860E7237349356C7DC23A419FE0E215ECFD24DD5AE5E59D6B68CA171007891F9632F3B0D075838FA29540A4F3AE842EED7CA920F33633095A9AB489610A0131A1013AD4D2CCF00A8A6FB1943A392A489AB7507CF65AFFA31B4DB14851AE0115F9119F4FBFCB6587DE8EEFBB886DDC106C95BF697E1D9DF3DAF899FD67A942922EE79AE5CF41FEE42F50E537E67',16)
_, r, s = gmpy2.gcdext(e1, e2)
m = pow(c1, r, n) * pow(c2, s, n) % n
print long_to_bytes(m)
2.8 低解密指数攻击
在RSA中d也称为揭秘指数,当d比较小的时候,e就显得特别大了。使用情况e过大或过小,在e过大或者过小的情况下,可使用算法快速推断出d的值,进而求出m。
例如题目:
n = 460657813884289609896372056585544172485318117026246263899744329237492701820627219556007788200590119136173895989001382151536006853823326382892363143604314518686388786002989248800814861248595075326277099645338694977097459168530898776007293695728101976069423971696524237755227187061418202849911479124793990722597L
e = 354611102441307572056572181827925899198345350228753730931089393275463916544456626894245415096107834465778409532373187125318554614722599301791528916212839368121066035541008808261534500586023652767712271625785204280964688004680328300124849680477105302519377370092578107827116821391826210972320377614967547827619L
c = 38230991316229399651823567590692301060044620412191737764632384680546256228451518238842965221394711848337832459443844446889468362154188214840736744657885858943810177675871991111466653158257191139605699916347308294995664530280816850482740530602254559123759121106338359220242637775919026933563326069449424391192
求明文m?
这个题需要一个GitHub上的工具RSA-wiener-attack,脚本中利用到了其中的一个库,所以这个脚本需要放到工具文件夹中执行。
工具了链接:
https://github.com/pablocelayes/rsa-wiener-attack
解题脚本如下:
#!/usr/bin/python
#coding:utf-8
import gmpy2
from Crypto.PublicKey import RSA
import ContinuedFractions, Arithmetic
from Crypto.Util.number import long_to_bytes
def wiener_hack(e, n):
frac = ContinuedFractions.rational_to_contfrac(e, n)
convergents = ContinuedFractions.convergents_from_contfrac(frac)
for (k, d) in convergents:
if k != 0 and (e * d - 1) % k == 0:
phi = (e * d - 1) // k
s = n - phi + 1
discr = s * s - 4 * n
if (discr >= 0):
t = Arithmetic.is_perfect_square(discr)
if t != -1 and (s + t) % 2 == 0:
print("Hacked!")
return d
return False
def main():
n = 460657813884289609896372056585544172485318117026246263899744329237492701820627219556007788200590119136173895989001382151536006853823326382892363143604314518686388786002989248800814861248595075326277099645338694977097459168530898776007293695728101976069423971696524237755227187061418202849911479124793990722597L
e = 354611102441307572056572181827925899198345350228753730931089393275463916544456626894245415096107834465778409532373187125318554614722599301791528916212839368121066035541008808261534500586023652767712271625785204280964688004680328300124849680477105302519377370092578107827116821391826210972320377614967547827619L
c = 38230991316229399651823567590692301060044620412191737764632384680546256228451518238842965221394711848337832459443844446889468362154188214840736744657885858943810177675871991111466653158257191139605699916347308294995664530280816850482740530602254559123759121106338359220242637775919026933563326069449424391192
d = wiener_hack(e, n)
m = pow(c,d,n)
print long_to_bytes(m)
if __name__=="__main__":
main()

2.9 根据公钥计算得到私钥
这种题目需要使用工具RsaCtfTools根据公钥生成私钥
题目只给出了2个文件,1个私钥文件和1个密文文件。
按照常规查看提取一下公钥文件,发现n特别大,无法直接分解,而且e也不存在是特殊值的可能,也不存在其他的攻击方法,只能考虑这个“根据公钥计算得到私钥的方法”了,似乎这是爆解。
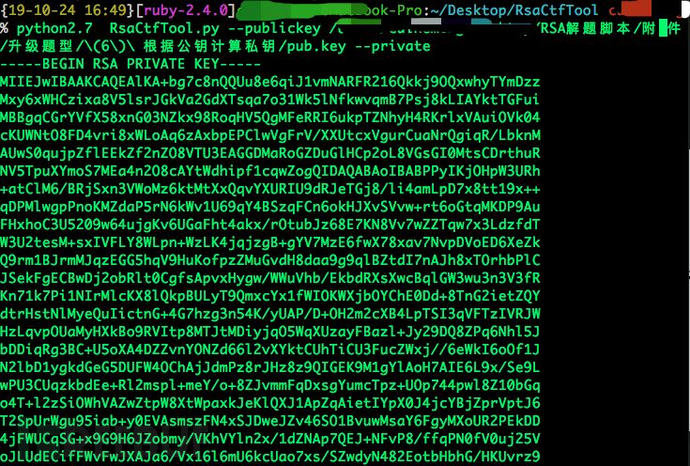
这是生成的私钥
把这个私钥命名保存为pri.key然后用openssl解出来就好
openssl rsautl -decrypt -inkey pri.key -in enc1 -out 123.txt
解出来的flag就保存到123.txt中了;
2.10 分解n得到相同的几个p
分解n得到k个p即n=p**k
由欧拉函数得:
phi=(p**k)-(p**k-1)
d = gmpy2.invert(e,phi)
m=pow(enc,d,n)
欧拉函数学习链接:
https://blog.csdn.net/liuzibujian/article/details/81086324
题目中幂使用的是r而不是k,(python中使用**代表多少次幂)
首先打开题目发现给了e和n还有enc,然后这个n使用factordb分解一下,发现分解出来4个一样的q。解题脚本如下。
#!/usr/bin/python
#coding:utf-8
import base64
import gmpy2
import libnum
from Crypto.Util.number import long_to_bytes,bytes_to_long
c = "YXmuOsaD1W4poLAG2wPrJ/nYZCkeOh2igCYKnZA6ecCeJadT6B3ZVTciPN6LJ8AcAsRXNnkC6+9PNJPhmosSG5UGGbpIcg2JaZ1iA8Sm3fGiFacGvQsJOqqIWb01rjaQ3rDBKB331rrNo9QNOfMnjKr0ejGG+dNObTtvnskICbYbNnSxMxLQF57H5JnWZ3LbbKQ493vmZzwvC6iH8blNPAp3dBlVzDqIAmxmUbk0OzFjPoHphD1oxHdzXyQNW+sLxVldrf9xcItq92jN5sqBYrG8wADIqY1/sqhTMZvkIYFMHqoMQuiRSnVrCF2h2RtGDEayLo0evgXI/0W3YveyKCHViOnG6wypcBFm九1ZWdjp3fVW/4DyxW6xu9hg/NlXyRP6pT/OyQpcyTqKRuiXJLWgFUJI/8TRgyAjBLLgSd3U0N3VM8kewXw5j+fMUTCW9/Gy4iP8m52Zabx/vEKdwdGZ0QyvgvAWGUFZ96EK0g1BM/LU9Tuu2R+VKcCSCprg283x6NfYxmU26KlQE6ZrrjLmbCOe0327uaW9aDbLxZytPYIE5ZkzhSsD9JpQBKL30dCy3UKDbcuNgB6SrDddrbIuUd0/kLxuwh6kTqNbC4NDrOT4WAuP4se8GGOK8Wz0dL6rE6FkzMnI4Qg501MTSNQZ4Bp7cNf6H9lTa/4DNOl0="
e = 58134567416061346246424950552806959952164141873988197038339318172373514096258823300468791726051378264715940131129676561677588167620420173326653609778206847514019727947838555201787320799426605222230914672691109516799571428125187628867529996213312357571123877040878478311539048041218856094075106182505973331343540958942283689866478426396304208219428741602335233702611371265705949787097256178588070830596507292566654989658768800621743910199053418976671932555647943277486556407963532026611905155927444039372549162858720397597240249353233285982136361681173207583516599418613398071006829129512801831381836656333723750840780538831405624097443916290334296178873601780814920445215584052641885068719189673672829046322594471259980936592601952663772403134088200800288081609498310963150240614179242069838645027877593821748402909503021034768609296854733774416318828225610461884703369969948788082261611019699410587591866516317251057371710851269512597271573573054094547368524415495010346641070440768673619729280827372954003276250541274122907588219152496998450489865181536173702554116251973661212376735405818115479880334020160352217975358655472929210184877839964775337545502851880977049299029101466287659419446724781305689536816523774995178046989696610897508786776845460908137698543091418571263630383061605011820139755322231913029643701770497299157169690586232187419462594477116374977216427311975598620616618808494138669546120288334682865354702356192972496556372279363023366842805886601834278434406709218165445335977049796015123909789363819484954615665668979
p = 165740755190793304655854506052794072378181046252118367693457385632818329041540419488625472007710062128632942664366383551452498541560538744582922713808611320176770401587674618121885719953831122487280978418110380597358747915420928053860076414097300832349400288770613227105348835005596365488460445438176193451867
n = p**4
phi = p**4-p**3
c = bytes_to_long(c.decode('base64'))
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print long_to_bytes(m)
2.11 已知n,e,d求p,q
这个题就是知道n但是分解不出p,q来,题目给了加密脚本,把输出的值也给了,里面有n,e,d
这是加密脚本:
from gmpy2 import invert
from md5 import md5
from secret import p, q
e = 65537
n = p*q
phi = (p-1)*(q-1)
d = invert(e, phi)
print n, e, d
print "Flag: flag{%s}" %md5(str(p + q)).hexdigest()
然后n发现没发用factordb去分解出来所以只能用脚本去跑了,解题脚本如下。
#!/usr/bin/python
#coding:utf-8
import random
from md5 import md5
def gcd(a, b):
if a < b:
a, b = b, a
while b != 0:
temp = a % b
a = b
b = temp
return a
def getpq(n,e,d):
p = 1
q = 1
while p==1 and q==1:
k = d * e - 1
g = random.randint ( 0 , n )
while p==1 and q==1 and k % 2 == 0:
k /= 2
y = pow(g,k,n)
if y!=1 and gcd(y-1,n)>1:
p = gcd(y-1,n)
q = n/p
return p,q
def main():
n = 16352578963372306131642407541567045533766691177138375676491913897592458965544068296813122740126583082006556217616296009516413202833698268845634497478988128850373221853516973259086845725813424850548682503827191121548693288763243619033224322698075987667531863213468223654181658012754897588147027437229269098246969811226129883327598021859724836993626315476699384610680857047403431430525708390695622848315322636785398223207468754197643541958599210127261345770914514670199047435085714403641469016212958361993969304545214061560160267760786482163373784437641808292654489343487613446165542988382687729593384887516272690654309
e = 65537
d = 9459928379973667430138068528059438139092368625339079253289560577985304435062213121398231875832264894458314629575455553485752685643743266654630829957442008775259776311585654014858165341757547284112061885158006881475740553532826576260839430343960738520822367975528644329172668877696208741007648370045520535298040161675407779239300466681615493892692265542290255408673533853011662134953869432632554008235340864803377610352438146264524770710345273439724107080190182918285547426166561803716644089414078389475072103315432638197578186106576626728869020366214077455194554930725576023274922741115941214789600089166754476449453
p,q = getpq(n,e,d)
print p
print q
print "Flag: flag{%s}" %md5(str(p + q)).hexdigest()
if __name__ == '__main__':
main()
2.12 低加密指数攻击
广播攻击
适用情况:模数n、密文c不同,明文m、加密指数e相同。一般会是e=k,然后给k组数据
使用不同的模数n,相同的公钥指数e加密相同的信息。就会得到多个(m^e) ==ci (mod ni),将(m^e)视为一个整体M,这就是典型的中国剩余定理适用情况。按照本文的中国剩余定理小节容易求得m^e的值,当e较小时直接开e方即可,可使用gmpy2.iroot(M,e)方法。
题目:
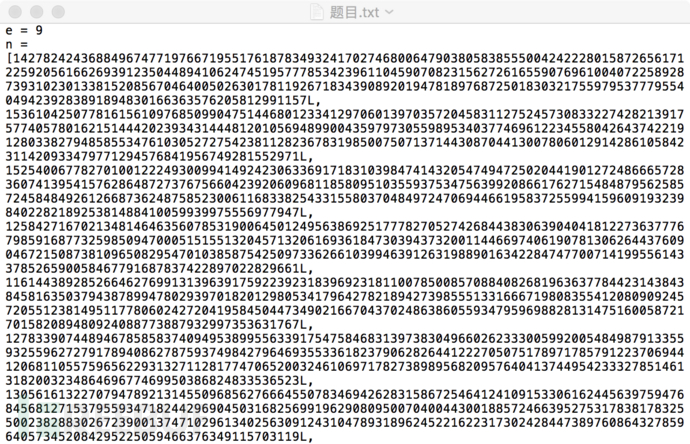
解题脚本:
#!/usr/bin/python
#coding:utf-8
import gmpy2
import time
from Crypto.Util.number import long_to_bytes
def CRT(items):
N = reduce(lambda x, y: x * y, (i[1] for i in items))
result = 0
for a, n in items:
m = N / n
d, r, s = gmpy2.gcdext(n, m)
if d != 1: raise Exception("Input not pairwise co-prime")
result += a * s * m
return result % N, N
# 读入 e, n, c
e = 9
n = [142782424368849674771976671955176187834932417027468006479038058385550042422280158726561712259205616626939123504489410624745195777853423961104590708231562726165590769610040722589287393102301338152085670464005026301781192671834390892019478189768725018303217559795377795540494239283891894830166363576205812991157L, 153610425077816156109768509904751446801233412970601397035720458311275245730833227428213917577405780162151444202393431444812010569489900435979730559895340377469612234558042643742219128033827948585534761030527275423811282367831985007507137144308704413007806012914286105842311420933479771294576841956749281552971L, 152540067782701001222493009941492423063369171831039847414320547494725020441901272486665728360741395415762864872737675660423920609681185809510355937534756399208661762715484879562585724584849261266873624875852300611683382543315580370484972470694466195837255994159609193239840228218925381488410059939975556977947L, 125842716702134814646356078531900645012495638692517778270527426844383063904041812273637776798591687732598509470005151551320457132061693618473039437320011446697406190781306264437609046721508738109650829547010385875425097336266103994639126319889016342284747700714199556143378526590058467791687837422897022829661L, 116144389285266462769913139639175922392318396923181100785008570884082681963637784423143843845816350379438789947802939701820129805341796427821894273985551331666719808355412080909245720551238149511778060242720419584504473490216670437024863860559347959698828131475160058721701582089480924088773887932997353631767L, 127833907448946785858374094953899556339175475846831397383049660262333005992005484987913355932559627279178940862787593749842796469355336182379062826441222705075178971785791223706944120681105575965622931327112817747065200324610697178273898956820957640413744954233327851461318200323486469677469950386824833536523L, 130561613227079478921314550968562766645507834694262831586725464124109153306162445639759476845681271537955934718244296904503168256991962908095007040044300188572466395275317838178325500238288302672390013747102961340256309124310478931896245221622317302428447389760864327859640573452084295225059466376349115703119L, 115953389401040751013569404909249958538962411171147823610874077094621794755967854844224923689925397631692572916641171075740839099217316101334941033937183815345038898177087515909675028366437302462022970987947264115373697445950951595479758872029099661065186221250394358255523574834723958546450323357472451930993L, 143437107845384843564651522639125300763388830136500260725097766445883003928355325003575359566631064630487365774344508496878731109174874449170057678821440711511966073934025028100604234445470976333825866939923998344367645612128590820812489407412175198698290167077116185959180877334222693344630253253476594907313L]
c = [85033868418784308573673709960700777350314426427677627319697346811123742342359072170220428874952996988431950989321281905284522596263957356289624365171732095210045916218066135140320107686084053271623461104022705353814233772164502775939590711842361956121603943483040254727995655776263673058788416722141673409688L, 66065963470666895005407449599703926269325406456711861190876894466341571726360462706664546294453572319565476664348345756905411939632955966517708138047546806602828064213238537646393524578984547577761559965654539771172357089802682793169968961304179886652390277814477825753096636750388350662980872556701402397564L, 116011740820520887443111656288411611070614127688662643257265381793048354928820176624229624692124188995846076431510548507016903260774215950803926107831505634778278712070141663189086436127990584944132764896694777031370995058271038329228336417590284517922855284619653301817355115583540545182119702335431334401666L, 97640420284096094887471273365295984332267897927392169402918423863919914002451127544715668846623138003564829254309568918651163254043205129883843425179687841236818720463784828905460885026290909768599562386370732119591181513319548915478512030197629196018254041500662654260834562708620760373487652389789200792120L, 8112507653841374573057048967617108909055624101437903775740427861003476480616929517639719198652146909660899632120639789106782550275648578142883715280547602249589837441805676364041484345030575130408744621981440093280624046635769338568542048839419939250444929802135605724150484414516536378791500915047844188300L, 36792148360808115566234645242678223867680969786675055638670907933041180936164293809961667801099516457636164692292891528415720085345494773373966277807505798679784807614784581861287048096977968620964436947452527540958289441390882589051225367658014709290392321808926567572528170531844664734909469690750971883323L, 53043093283305492238903255767698153246673671181809989362223466090875767705978690531154079519999671834688647277179370374802495005937892824566602423646978168777735383632928274082669949750078161820002768640908750005814934158829006019656592134357897586040866207754535586785064545866404380204728594863102313407789L, 88499407133762624445946519155722583633934260410706930537441122463087556094734626189377091740335667052378955691250910459790202385799502439716173363179773811920751410726795431402796346647688144853156900427797933862087074385441977254140336390678022955770879265490567987868532251217565094093318626424653599450992L, 138337520305048557335599940473834485492131424901034295018189264168040969172072024612859307499682986987325414798210700710891033749119834960687318156171051379643844580970963540418974136891389303624057726575516576726845229494107327508855516437230240365759885913142671816868762838801720492804671259709458388192984L]
data = zip(c, n)
x, n = CRT(data)
m = gmpy2.iroot(gmpy2.mpz(x), e)[0].digits()
print long_to_bytes(m)
2.13 知道只知道e,n切n无法分解,e非常大
这是在buu遇到的一个rsa很有意思,需要用到工具rsa-wiener-attack-master
题目给了一个py文件
N = 101991809777553253470276751399264740131157682329252673501792154507006158434432009141995367241962525705950046253400188884658262496534706438791515071885860897552736656899566915731297225817250639873643376310103992170646906557242832893914902053581087502512787303322747780420210884852166586717636559058152544979471
e = 46731919563265721307105180410302518676676135509737992912625092976849075262192092549323082367518264378630543338219025744820916471913696072050291990620486581719410354385121760761374229374847695148230596005409978383369740305816082770283909611956355972181848077519920922059268376958811713365106925235218265173085
#d=8920758995414587152829426558580025657357328745839747693739591820283538307445
import hashlib
flag = "flag{" + hashlib.md5(hex(d)).hexdigest() + "}"
#print flag
注释的是我后来改的,这里给了n和e还都特别大,n也没法分解,于是就用到工具了,在这个工具中吧e,n换上去,可以得到d,有了d以后就可以直接利用这个题目的脚本跑出flag了,这里考点就是在不能分解n的情况下,去利用e太大这一点去求d,e太大 可使用算法从e中快速推断出d的值。 可使用Wiener’s Attack进行解d。
00x3 RSA混合题目
3.1 base64隐写+共模攻击
这是buu的一道密码题叫rsa&what;
首先题目给的很充足了,加密脚本还有加密后的得到的文件,n,e,c都写进去了。呢么我们先来看加密脚本。
from Crypto.Util.number import bytes_to_long, getPrime
from random import randint
from gmpy2 import powmod
p = getPrime(2048)
q = getPrime(2048)
N = p*q
Phi = (p-1)*(q-1)
def get_enc_key(N,Phi):
e = getPrime(N)
if Phi % e == 0:
return get_enc_key(N, Phi)
else:
return e
e1 = get_enc_key(randint(10, 12), Phi)
e2 = get_enc_key(randint(10, 12), Phi)
fr = open(r"./base64", "rb")#flag is in this file
f1 = open(r"./HUB1", "wb")
f2 = open(r"./HUB2", "wb")
base64 = fr.read(255)
f1.write("%d\n%d\n" % (N, e1))
f2.write("%d\n%d\n" % (N, e2))
while len(base64)>0:
pt = bytes_to_long(base64)
ct1 = powmod(pt, e1, N)
ct2 = powmod(pt, e2, N)
f1.write("\n%d" % ct1)
f2.write("\n%d" % ct2)
base64 = fr.read(255)
fr.close()
f1.close()
f2.close()
很明显了,这里从未给出的文件中读取了明文,经过加密输出了n,e,c但是这里有个小坑,他的c是255位一组来做的,所以不能把所有的c一股脑的解码,需要一段一段的解码然后把这解出来的base64放到一个txt中然后利用base64隐写来解就行了。解题脚本如下。
#!/usr/bin/python
#coding:utf-8
import re
import gmpy2
from Crypto.Util.number import long_to_bytes
import base64
e1 = 1697
e2 = 599
n = 785095419718268286866508214304816985447077293766819398728046411166917810820484759314291028976498223661229395009474063173705162627037610993539617751905443039278227583504604808251931083818909467613277587874545761074364427549966555519371913859875313577282243053150056274667798049694695703660313532933165449312949725581708965417273055582216295994587600975970124811496270080896977076946000102701030260990598181466447208054713391526313700681341093922240317428173599031624125155188216489476825606191521182034969120343287691181300399683515414809262700457525876691808180257730351707673660380698973884642306898810000633684878715402823143549139850732982897459698089649561190746850698130299458080255582312696873149210028240898137822888492559957665067936573356367589784593119016624072433872744537432005911668494455733330689385141214653091888017782049043434862620306783436169856564175929871100669913438980899219579329897753233450934770193915434791427728636586218049874617231705308003720066269312729135764175698611068808404054125581540114956463603240222497919384691718744014002554201602395969312999994159599536026359879060218056496345745457493919771337601177449899066579857630036350871090452649830775029695488575574985078428560054253180863725364147
c1=36869806815936046911848195817405817350259890871483063184373728397968909458432625046025376290214729914038387534731762237978339011724858818860181178811639468996206294711495853807311240013786226884265118119546377272154555615363105236192878292703331473547623021744317034819416624562896226194523639793573028006666236271812390759036235867495803255905843636447252225413871038762657801345647584493917576263471587347202664391908570140389126903204602391093990827188675090199750617303773574821926387194478875191828814971296674530519321530805302667925998711835019806761133078403281404889374663875077339168901297819436499920958268483684335998301056068380228873524800383911402490807139268964095165069610454677558808756444381542173782815227920906224931028457073652453777424387873533280455944646592996920617956675786286711447540353883400282402551158169958389450168079568459656526911857835375748015814860506707921852997096156275804955989964215077733621769938075413007804223217091604613132253046399456747595300404564172224333936405545921819654435437072133387523533568472443532200069133022979195685683508297337961701169394794966256415112246587706103819620428258245999539040721929317130088874161577093962579487428358736401687123174207198251449851429295
c2=271453634732502613378948161256470991260052778799128789839624515809143527363206813219580098196957510291648493698144497567392065251244844074992734669490296293997386198359280316655904691639367482203210051809125904410431506925238374843856343243276508280641059690938930957474434518308646618959004216831130099873532714372402117796666560677624822509159287675432413016478948594640872091688482149004426363946048517480052906306290126242866034249478040406351940088231081456109195799442996799641647167552689564613346415247906852055588498305665928450828756152103096629274760601528737639415361467941349982213641454967962723875032638267311935042334584913897338553953961877439389588793074211502597238465542889335363559052368180212013206172712561221352833891640659020253527584706465205486408990762759230842192028381048563437724528409174790022752557512795782713125166158329880702730769957185428522011430144840232256419113631679343171680631630775266488738173707357123139368825087043785842169049943237537188129367275730984789479909103397937113837824575137021012333461552176687570010445744268373840742899299977372834041925102853718964831225250407279578465008537542659673685686242773379131904890865110699190451534445434533919127658976874721029586168106207
_, r, s = gmpy2.gcdext(e1, e2)
m = pow(c1, r, n) * pow(c2, s, n) % n
print long_to_bytes(m)
zz=long_to_bytes(m)
open('tmp.txt','a').write(long_to_bytes(m))
这是解rsa密码,c一共6组,这是第一组。之后解完了在用base64隐写解密脚本:
# -*- coding: cp936 -*-
b64chars = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/'
with open('tmp.txt', 'rb') as f:
bin_str = ''
for line in f.readlines():
stegb64 = ''.join(line.split())
rowb64 = ''.join(stegb64.decode('base64').encode('base64').split())
offset = abs(b64chars.index(stegb64.replace('=','')[-1])-b64chars.index(rowb64.replace('=','')[-1]))
equalnum = stegb64.count('=') #no equalnum no offset
if equalnum:
bin_str += bin(offset)[2:].zfill(equalnum * 2)
print ''.join([chr(int(bin_str[i:i + 8], 2)) for i in xrange(0, len(bin_str), 8)])
0x04 总结
RSA的题目用来作为密码学的入门还是比较友好的,这些只是一些比较常见的题目总结,还有很多更有意思的玩法大家可以在以后的比赛或者做题中慢慢挖掘。
如需授权、对文章有疑问或需删除稿件,请联系 FreeBuf 客服小蜜蜂(微信:freebee1024)
 网络实战攻防
网络实战攻防










