 LEdge1
LEdge1- 关注
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
有些时候二维码被严重破坏导致无法扫描,促使我去学习了一波关于二维码的知识。二维码一共有40个尺寸。V 1是21 x 21的矩阵,V2是 25 x 25的矩阵,V3是29的尺寸,每增加一个等级,就会增加4的尺寸,公式是:(V-1)*4 + 21 最高V 40,(40-1)*4+21 = 177,所以最高是177 x 177 的正方形。
二维码格式示例如下: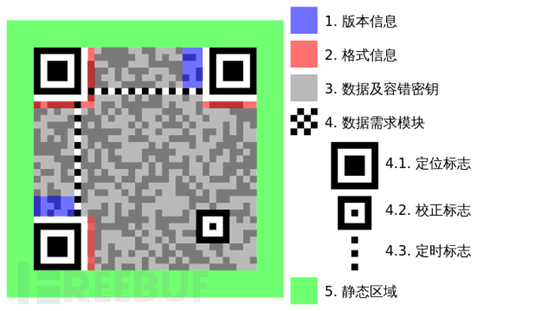
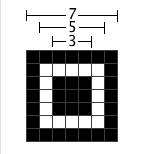
定位图案
定位图案,就是每个二维码都有的左上、左下和右上三个角的“回”字形的标志。用于标记二维码的矩形大小他的尺寸都是7*7的模块。
 功能性数据:存在于所有的尺寸中,用于存放一些格式化数据的,主要内容为“纠错码等级(3bit)+掩码类别(2bit)+BCH code(10bit,用于纠错)”,然后这15个bits还要与101010000010010做XOR操作,主要是为了如果选用了00的纠错级别和000的Mask,从而造成全部为白色,这会增加扫描器的图像识别的困难。比如:
功能性数据:存在于所有的尺寸中,用于存放一些格式化数据的,主要内容为“纠错码等级(3bit)+掩码类别(2bit)+BCH code(10bit,用于纠错)”,然后这15个bits还要与101010000010010做XOR操作,主要是为了如果选用了00的纠错级别和000的Mask,从而造成全部为白色,这会增加扫描器的图像识别的困难。比如:
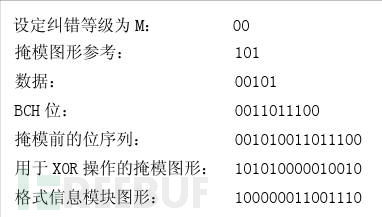 而这15个bit在format information区域内的分布如下:
而这15个bit在format information区域内的分布如下:
 在 Version 7以上,需要预留两块3 x 6的区域存放一些版本信息。
在 Version 7以上,需要预留两块3 x 6的区域存放一些版本信息。
数据码和纠错码
除了上述的那些地方,剩下的地方存放 数据码 和纠错码。就是最前面两张图的深灰色区域,一般数据都是从右下角开始填充,先填充数据码,数据码填充完毕之后再填充纠错码,以v1为例,数据的填充顺序,是这样的:
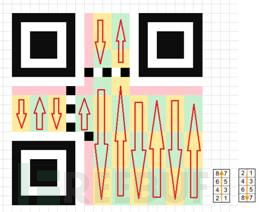
数据编码
QR码支持如下的编码:
数字编码:从0到9;
字符编码:包括 0-9,大写的A到Z(没有小写),以及符号$ % * + – . / : 包括空格;
字节编码:可以是0-255的ISO-8859-1字符;
日文编码:也是双字节编码;
Extended ChannelInterpretation (ECI) mode 主要用于特殊的字符集。并不是所有的扫描器都支持这种编码;
Structured Appendmode 用于混合编码,也就是说,这个二维码中包含了多种编码格式;
FNC1 mode 这种编码方式主要是给一些特殊的工业或行业用的。比如GS1条形码之类的
下表是每个模式的编码相对应的“编号”,这个编号,存在于format information区域。
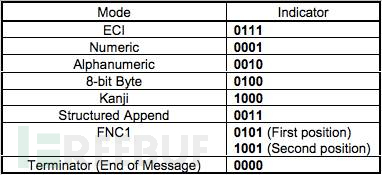
因为种类较多较复杂,而且为了方便大家理解,我们在这里值选择数字编码和字符编码举例,其它的编码,有兴趣的同学可以查看官方文档。
示例一:
数字编码,从0到9。如果需要编码的数字的个数不是3的倍数,那么,最后剩下的1或2位数会被转成4或7bits,则其它的每3位数字会被编成10位的二进制数,最后将这些二进制数据连接起来并在前面加上编码模式的编号和字符计数指示符(就是表示了被编码的信息有多少个字符),字符计数指示符的长度取决于编码的模式和所要编成二维码的版本,在数字编码中,字符计数指示符如下表对应的有10、12或14位:
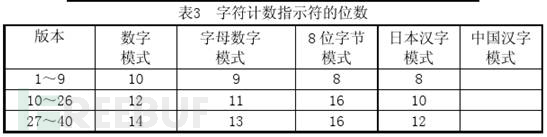
比如在Version 1的尺寸下,纠错级别为H(纠错级别我们会在下面讲到)的情况下,我们要编码: 01234567
(1)把上述数字分成三组: 012 345 67
(2)把他们转成10bit二进制: 012 转成 0000001100;345 转成 0101011001;67 转成1000011。
(3)把这三个二进制串起来: 0000001100 0101011001 1000011
(4)把数字的个数转成二进制 (version 1-H是10 bits ): 8个数字的二进制是0000001000
(5)把数字编码的标志0001和第4步的编码加到前面: 0001 00000010000000001100 0101011001 1000011
示例二:
字符编码(也叫字母数字编码)。包括 0-9,大写的A到Z(没有小写),以及符号$ % *+ – . / : 包括空格。这些字符会映射成一个字符索引表。如下所示(两个表,中英文对照):(其中的SP是空格,Char是字符,Value是其索引值),编码的过程是把字符两两分组,然后转成下表的45进制,然后转成11bits的二进制,如果最后有一个落单的,那就转成6bits的二进制。而字符计数指示符需要根据不同的Version尺寸编成9, 11或13个二进制(如上表)。
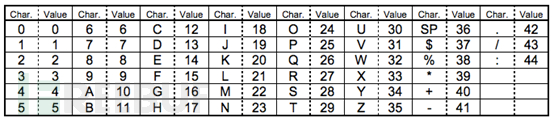
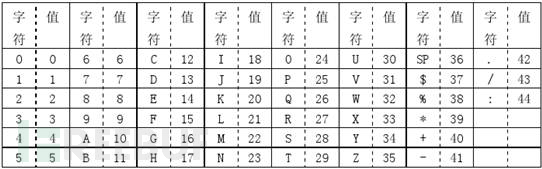
在V 1的尺寸下,纠错级别为H的情况下,编码: AC-42
(1)从字符索引表中找到 AC-42 这五个字条的索引 (10,12,41,4,2)
(2)两两分组: (10,12) (41,4) (2)
(3)把每一组转成11bits的二进制:(10,12) 10*45+12 = 462 转成 00111001110;(41,4)41*45+4 = 1849 转成 11100111001;
(4)把这些二进制连接起来:00111001110 11100111001 000010
(5)把字符的个数转成二进制 (Version 1-H为9 bits ): 5个字符,5转成 000000101
(6)在头上加上编码标识 0010 和第5步的个数编码: 0010 00000010100111001110 11100111001 000010
结束符和补齐符
以上述示例一为基础,在编码结束后,我们得到了如下编码:
然后,我们还要加上结束符,表示真正的额数据已经结束。
| 编码 | 字符数 | HELLO WORLD的编码 |
|---|---|---|
| 0010 | 000001011 | 01100001011 01111000110 10001011100 10110111000 10011010100 001101 |
我们还要加上结束符:
| 编码 | 字符数 | HELLO WORLD的编码 | 结束 |
|---|---|---|---|
| 0010 | 000001011 | 01100001011 01111000110 10001011100 10110111000 10011010100 001101 | 0000 |
按每组8个bit分组,如果所有的编码加起来不是8个倍数我们还要在后面加上足够的0,比如上面一共有45个bit,所以,我们还要加上3个0,然后按8个bits分好组:0001000000100000 00001100 01010110 01100001 10000000
接着就是补齐符,如果还没有达到我们最大的bits数的限制,我们还要加一些补齐码就是重复下面的两个bytes:11101100 00010001。(使用这两个字节的主要原因是,为了防止在填入数据时出现大片的深色或浅色区域,对扫描器产生干扰,使得二维码难以正常扫描),至于要补多少个补齐符,需要查看文档中相应的字符数和数据容量对应表,在官方文档中,相对应的是表7-表11
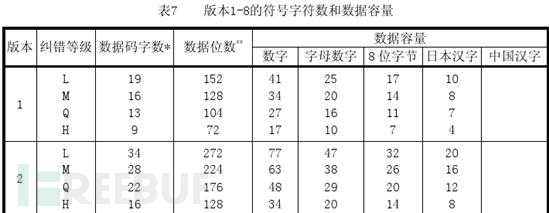
从表中,我们可以知道,v1-H的数据容量为9个数据码字(每个数据码字为8位),而我们上面已经有了6个数据码字,所以要补充三个8bit,补充完毕如下:0001000000100000 0000110001010110 01100001 10000000 11101100 00010001 11101100 上面的每一组数据为一个数据码字,Data Codewords,现在也只是原始数据,还需要对其加上纠错码。
纠错码
上面我们提到了纠错级别,二维码中有四种级别的纠错(从低到高为L、M、Q、H),这就是为什么有人在二维码的中心位置加入图标,也依旧能够扫描(就是二维码残缺量不超过所对应的纠错等级能允许的范围时,使用扫描工具依旧能扫描出内容的原因)。
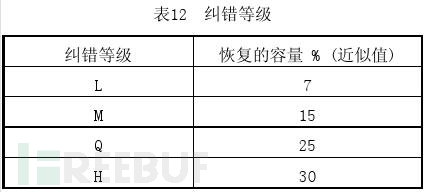
至于纠错码是如何计算的,这涉及到里德-所罗门纠错算法,里德-所罗门码是定长码。这个比较复杂,但是万能的Pythom里面有一个交reedsolo的库可以直接调用。这意味着一个固定长度输入的数据将被处理成一个固定长度的输出数据。在最常用的(255,223)里所码中,223个里德-所罗门输入符号(每个符号有8个 位元)被编码成255个输出符号。大多数里所错误校正编码流程是成体系的。这意味着输出的码字中有一部分包含着输入数据的原始形式。符号大小为8位元的里所码迫使码长(编码长度)最长为255个符号。标准的(255,223)里所码可以在每个码字中校正最多16个里所符号的错误。由于每个符号事实上是8个位元,这意味着这个码可以校正最多16个短爆发性错误。里德-所罗门码,如同卷积码一样,是一种透明码。这代表如果信道符号在队列的某些地方被反转,解码器一样可以工作。解码结果将是原始数据的补充。但是,里所码在缩短后会失去透明性。在缩短了的码中,“丢失”的比特需要被0或者1替代,这由数据是否需要补足而决定。(如果符号这时候反转,替代的0需要变成1)。这样就需要在里所解码前对数据进行强制性的侦测决定。
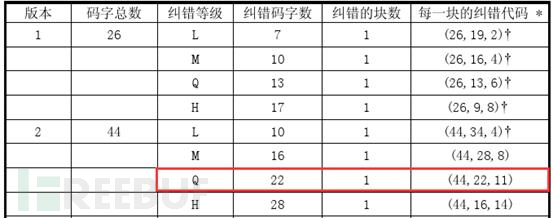
我们有现成的python模块来运算出纠错码——python的reedsolo模块。我们可以对照官方文档中的纠错特性表。以下表为例:
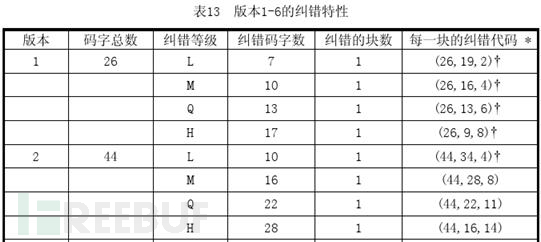
以版本1-H为例进行解释,从表中,我们可以清晰的知道,纠错码字数应该为17个,纠错的块数为1(表示这个版本要编码的数据只会分为一个数据块),(26,9,8)表示,这个版本的二维码总共可以存放26个码字,但是这26个码字中,有9个码字为数据码字,17个为纠错码字(8*2+1=17),8位纠错容量。每个表的下方否有注释信息:

这也是为什么纠错码字数为r*2,当后面有一个箭头时,表示r*2之后还要加1。在给数据码字添加纠错码时,还有对数据码字分块的操作,因为version1的二维码对数据码字之分一个块,不够明显,所以我们采用网上的一个例子:
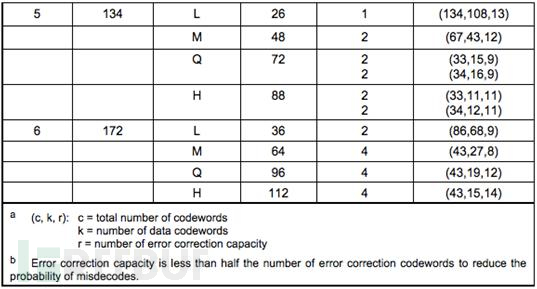 上述的Version 5 + Q纠错级:需要4个块(2个块为一组,共两组),头一组的两个Blocks中各15个字节(数据码字)数据 加上 各 9个字节的纠错容量(18个字节的纠错码字)。因为二进制写起来会让表格太大,所以,都用了十进制来表示,我们可以看到每一个数据块的纠错码有18个字节,也就是18个8bits的二进制数。
上述的Version 5 + Q纠错级:需要4个块(2个块为一组,共两组),头一组的两个Blocks中各15个字节(数据码字)数据 加上 各 9个字节的纠错容量(18个字节的纠错码字)。因为二进制写起来会让表格太大,所以,都用了十进制来表示,我们可以看到每一个数据块的纠错码有18个字节,也就是18个8bits的二进制数。
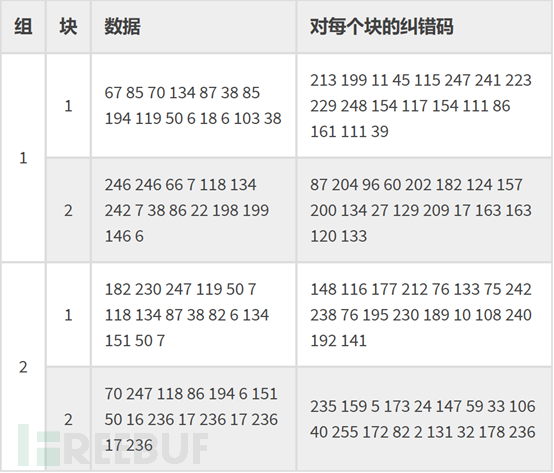
5. 最终编码,穿插放置。
此时,编码的过程,只剩下最后一步。
对于数据码字:把每个块的第一个codewords先拿出来按顺度排列好,然后再取第一块的第二个,如此类推。上述示例中的Data Codewords如下:
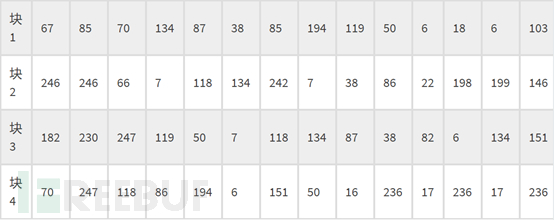
我们先取第一列的:67, 246 , 182 , 70
然后再取第二列的:67, 246, 182 , 70, 85,246 ,230 ,247
如此类推:67, 246, 182 , 70, 85,246 ,230 ,247 ……… ……… , 38 ,6,50, 17 ,7,236
对于纠错码,也是一样:
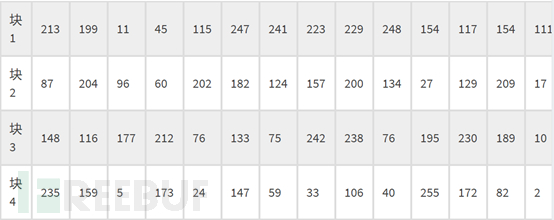
和数据码取的一样,得到:213,87,148,235,199,204,116,159,…… …… 39,133,141,236
然后,再把这两组放在一起(纠错码放在数据码之后)得到:
67, 246, 182, 70, 85, 246, 230, 247, 70, 66, 247, 118, 134, 7, 119, 86, 87,118, 50, 194, 38, 134, 7, 6, 85, 242, 118, 151, 194, 7, 134, 50, 119, 38, 87,16, 50, 86, 38, 236, 6, 22, 82, 17, 18, 198, 6, 236, 6, 199, 134, 17, 103, 146,151, 236, 38, 6, 50, 17, 7, 236, 213, 87, 148, 235, 199, 204, 116, 159, 11, 96,177, 5, 45, 60, 212, 173, 115, 202, 76, 24, 247, 182, 133, 147, 241, 124, 75,59, 223, 157, 242, 33, 229, 200, 238, 106, 248, 134, 76, 40, 154, 27, 195, 255,117, 129, 230, 172, 154, 209, 189, 82, 111, 17, 10, 2, 86, 163, 108, 131, 161,163, 240, 32, 111, 120, 192, 178, 39, 133, 141, 236剩余位
最后再加上Reminder Bits,对于某些Version的QR,上面的还不够长度,还要加上Remainder Bits,比如:上述的5Q版的二维码,还要加上7个bits,Remainder Bits加零就好了。关于哪些Version需要多少个Remainder bit,可以参看官方文档的表一(这里列出一部分)。
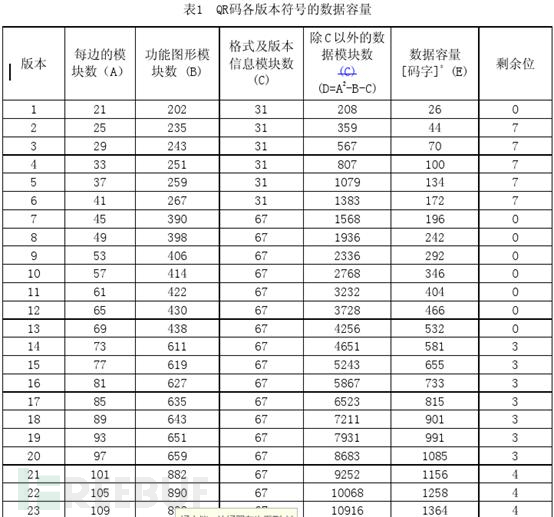
掩码(也叫掩模)
编码的步骤是完成了,但是要想生成一个完好的二维码,还需要先将现在所拥有的数据填入提前准备的空白模板后,选择一个合适的掩码,将原模板的数据与掩码进行异或运算,最后,再将format information填进去就生成了二维码。掩码存在的意义:二维码是要拿来扫描的,而扫描怕的就是无法清晰地分辨出编码信息的每一位。要是二维码中黑白点数量不均,或是空间分布不均都会导致大色块区域的出现,而大色块区域的出现会增加扫描时定位的难度,从而降低扫描的效率。更严重的情况下,如果数据填入后碰巧出现了功能性标识,比如定位标识的图样,还会干扰正常功能性标识的作用,导致QR码无法扫描。在计算机科学中,掩码就是一个二进制串,通过和数据进行异或运算来变换数据。在QR码中,掩码也是通过异或运算来变换数据矩阵。所以你可能已经猜到了,QR码的掩码就是预先定义好的矩阵。QR标准通过生成规则定义了八个数据掩码:
 前面的三位二进制的数据就是每个模式掩码相对应的编号,这个信息也是要填入format information中的。
前面的三位二进制的数据就是每个模式掩码相对应的编号,这个信息也是要填入format information中的。
 从这个图我们就可以直观的看到每种掩码的模板样子,以掩码2(编号为010)为例,j mod 3 = 0 就是表示从左变开始数,能被3整除的列,都要取逆(黑块变白块,白块变黑块),当然二维码的固定格式区域的信息时不用取逆的,所以要使用掩码2,需要取逆的列数为:0、3、6、9…..。
从这个图我们就可以直观的看到每种掩码的模板样子,以掩码2(编号为010)为例,j mod 3 = 0 就是表示从左变开始数,能被3整除的列,都要取逆(黑块变白块,白块变黑块),当然二维码的固定格式区域的信息时不用取逆的,所以要使用掩码2,需要取逆的列数为:0、3、6、9…..。
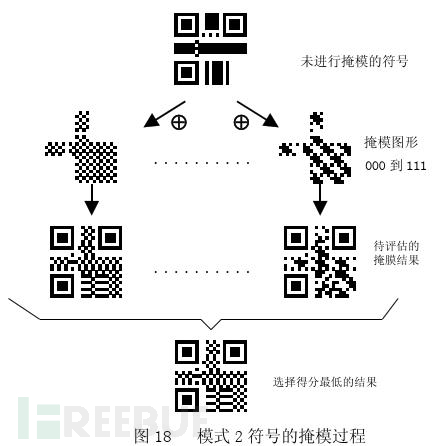 当然,官方规定在进行异或时,原始的数据模板要与每个掩码模板进行异或运算后,要进行如下的规则进行计分(处罚),最后选择分数最低的一个作为最佳的掩码选择。
当然,官方规定在进行异或时,原始的数据模板要与每个掩码模板进行异或运算后,要进行如下的规则进行计分(处罚),最后选择分数最低的一个作为最佳的掩码选择。
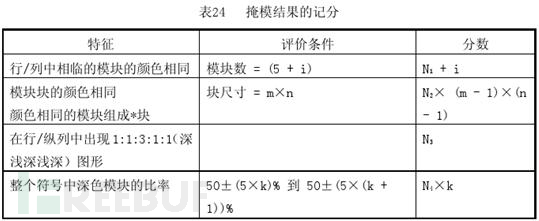
另外,使用python的reedsolo模块,能够在二维码损坏超出相应级别的容错范围时也能够恢复数据。
Python2环境下的reedsolo模块基本使用方式
1. 首先安装reedsolo模块,python官方下载的reedsolo模块版本为0.3,不是很好用,这次使用的reedsolo模块存放在下载包中的reedsolomon-master.zip,解压后在该路径下运行cmd命令python setup.py install即可。
 2. 进入python环境,导入reedsolo模块。定义一个对象,设置生成的纠错码个数为10个。
2. 进入python环境,导入reedsolo模块。定义一个对象,设置生成的纠错码个数为10个。
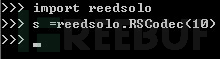 3. 为字符串“hello world”编码,生成纠错码。
3. 为字符串“hello world”编码,生成纠错码。

4. 进行解码
![]() 5. 现在大致了解了reedsolo模块的使用方法,那现在了解一下纠错码的作用,比如,我们现在将“hello world”写成错误的“hellx xorld”,这里我们出现了两个错误,配上之前生成的纠错码进行解码,输出的就是正确的字符串,纠错码就是这样了。
5. 现在大致了解了reedsolo模块的使用方法,那现在了解一下纠错码的作用,比如,我们现在将“hello world”写成错误的“hellx xorld”,这里我们出现了两个错误,配上之前生成的纠错码进行解码,输出的就是正确的字符串,纠错码就是这样了。
![]() 6. 纠错码算法是对所要纠错的内容一个字节一个字节地进行编码,所以编码后生成的是一个字节数组。
6. 纠错码算法是对所要纠错的内容一个字节一个字节地进行编码,所以编码后生成的是一个字节数组。
7. 将编码后的内容转化为十进制输出
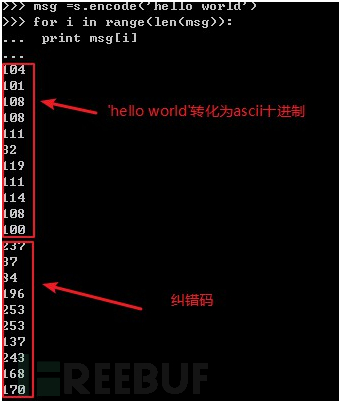
学以致用,复现MMA2015-MISC400-qr的二维码恢复挑战的解题步骤,原版write-up地址为:https://github.com/pwning/public-writeup/blob/master/mma2015/misc400-qr/writeup.md
1. 题目给出的二维码如下图

这是一个25*25的二维码,也就是version2的二维码,二位从它能看见的部分我们可以得到format information的一部分信息:??????011011010
2. 对照下面这个网址所给出的对应表,可以知道这个二维码使用了什么编码模式和使用了哪一个掩码
https://www.thonky.com/qr-code-tutorial/format-version-tables#list-of-all-format-information-strings
![]()
经对照可知,完整的format information信息应该是:010111011011010。且可以得到的信息还有该二维码使用的掩码为6,所对应的纠错等级为Q。
3. 将被遮挡的固定信息部分以及format information信息补充完整。
 与相对应的掩码进行异或运算,得到原始的数据中的一部分数据码字和纠错码字。下图就是掩码6相对应的图案。
与相对应的掩码进行异或运算,得到原始的数据中的一部分数据码字和纠错码字。下图就是掩码6相对应的图案。
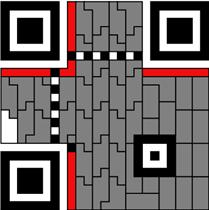
 4. 将掩码应用到我们补充完的二维码上,翻转与掩码中深色区域相对应的区域的颜色,并用灰色将format information覆盖,方便读取数据,如下图。
4. 将掩码应用到我们补充完的二维码上,翻转与掩码中深色区域相对应的区域的颜色,并用灰色将format information覆盖,方便读取数据,如下图。

5. 从右下角开始,按下图的蛇形顺序读取数据码字和纠错码字的信息,至于不同区域块的信息读取顺序,可以参考官方文档。
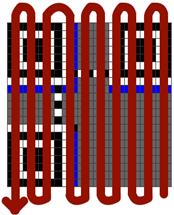
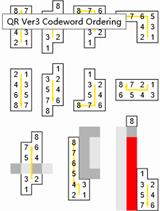
 且相对应的数据块分布应该如下图所示:
且相对应的数据块分布应该如下图所示:
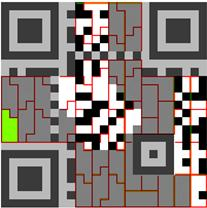
6. 将全部可读的信息读取出来:
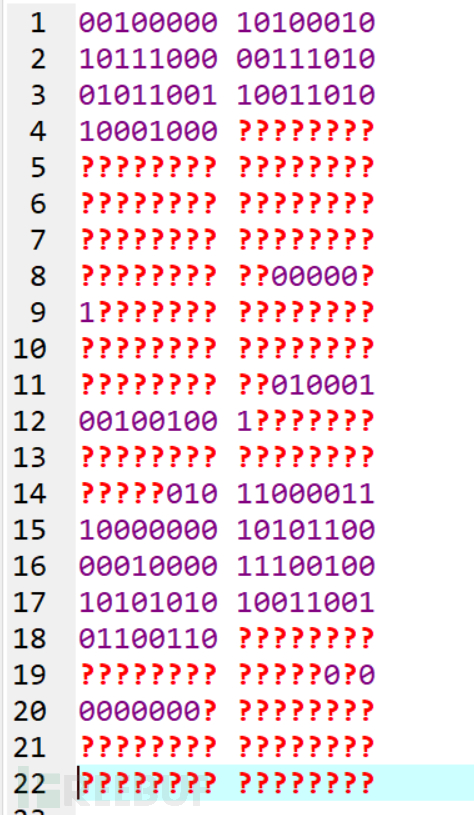
7. 根据官方文档的纠错特性表,可知version2-Q的纠错码字数有22个,数据码字数也有22个,在Q级别,它可以恢复不超过25%的损坏的字节,但是我们只有16个完整的字节,即超过63%的字节丢失,仔细查看Reed-Solomon的纠错能力,并意识到它可以纠正多达两倍的擦除——也就是说,如果 它知道错误在哪里,那么纠错能力就强得多。这意味着我们的代码可以从丢失的字节的50%恢复过来!但这意味着我们只能纠正多达22个丢失的字节,但是我们目前依然只有16个完整的字节,所以我们要想办法恢复一部分字节使得达到22个字节这个最低要求。
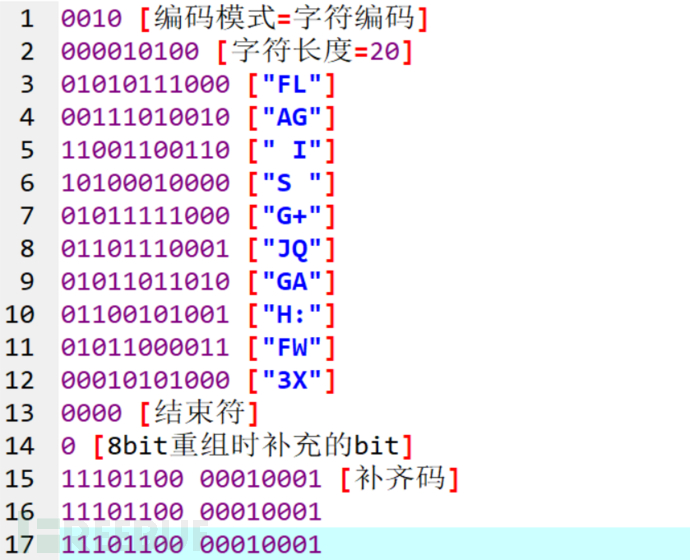
8. 我们先将获得的可读取数据整理一下:
0010:【编码模式=字符编码(字母数字模式)】
000010100:【9个bit长度的字符计数标识符=20个字符】
01010111000:【FL】
00111010010:【AG】
11001100110:【 I】
1010001000?:【S?】
我们计算一下,22个数据码字,就是176个bit,而20个字符,在编码的时候分为10组,每组11个bit,所以4+9+10*11=123个bit,123/8=15余3,再加上4个0(结束符) ,以及8bit重组时需要补充为8的倍数,8-3-4=1,所以还需要加1个0。这时候总共也就16个数据码字,22-16=6,所以还要加上6个 字节的 补齐码,如下(红色的是原本被遮住的数据):
00100000 10100010 10111000 00111010 01011001 10011010 10001000 ???????????????? ???????? ???????? ???????? ???????? ???????? ???????? ??000000 1110110000010001 11101100 00010001 11101100 00010001
这样,我们就回复了6个字节的数据,此时我们丢失的字节就只剩下22个了,正好达到了最低的要求。我们就可以使用纠错码恢复原本的数据。
9. 编写脚本利用python的reedsolo模块进行纠错。
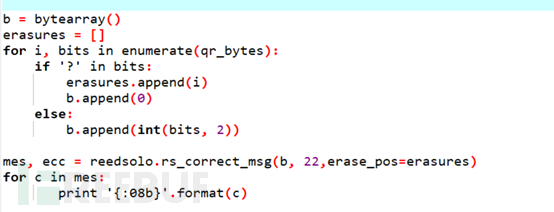
10. 得到全部的信息。
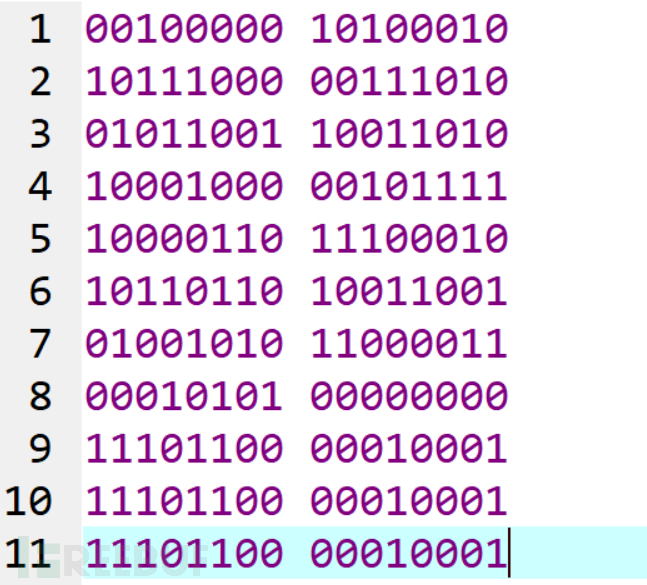
11. 拆分和解码
 参考文献:
参考文献:
https://zhuanlan.zhihu.com/p/21463650
https://coolshell.cn/articles/10590.html
官方文档(中文版):
https://wenku.baidu.com/view/ef77275f312b3169a451a4a4.html?pn=50
里德-所罗门码:
https://www.jianshu.com/p/8208aad537bb
https://en.wikiversity.org/wiki/Reed%E2%80%93Solomon_codes_for_coders#Encoding_outline
https://stackoverflow.com/questions/30363903/optimizing-a-reed-solomon-encoder-polynomial-division
MMA2015-MISC400-qr的write up:
https://github.com/pwning/public-writeup/blob/master/mma2015/misc400-qr/writeup.md
合天智汇:
http://www.hetianlab.com/expc.do?ec=ECID3581-0d42-4928-b602-ddd8e61b24a3
*本文作者:LEdge1,转载请注明来自FreeBuf.COM
如需授权、对文章有疑问或需删除稿件,请联系 FreeBuf 客服小蜜蜂(微信:freebee1024)











