 本文由
创作,已纳入「FreeBuf原创奖励计划」,未授权禁止转载
本文由
创作,已纳入「FreeBuf原创奖励计划」,未授权禁止转载
1.简介
如果在DES加密中两轮或两轮以上的子密钥泄漏,则几乎可以完全逆推出初始密钥。但由于有效位仅为56bit,所以密钥只能恢复56bit,还有剩下的8bit未知,但2^8 仅有256种情况,完全可以使用暴力破解。
然而暴力破解的前提是需要有一个标志来告诉我们结果是否准确,在有些情况中暴力破解的结果是没有办法判断准确与否的。
此处使用湖湘杯中的一道密码学题目来做示例,题目如下:
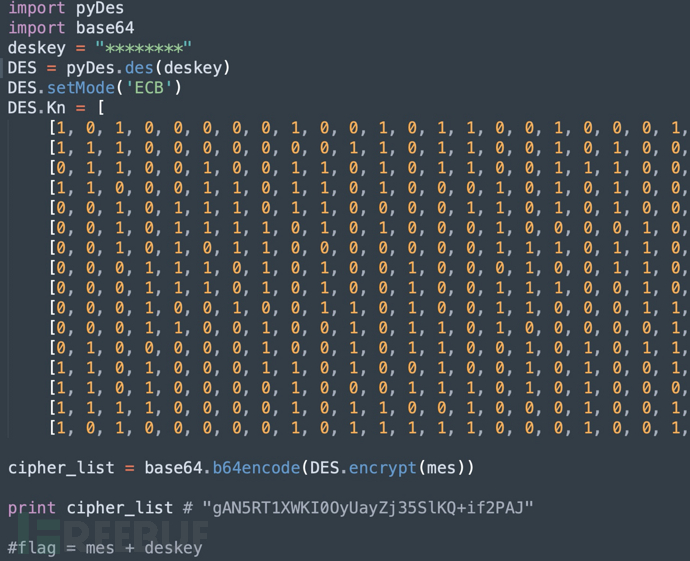
import pyDes
import base64
deskey = "********"
DES = pyDes.des(deskey)
DES.setMode('ECB')
DES.Kn = [
[1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0],
[1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0],
[0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0],
[1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1],
[0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1],
[0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0],
[0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0],
[0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0],
[0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0],
[0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0],
[0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1],
[0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0],
[1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0],
[1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1],
[1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1],
[1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0,1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1]]
cipher_list = base64.b64encode(DES.encrypt(mes))
print cipher_list # "gAN5RT1XWKI0OyUayZj35SlKQ+if2PAJ"
#flag = mes + deskey
可以看到题目中提供了DES的16轮子密钥,而题目要求将加密前的消息和DES key作为flag提交。
2.DES 子密钥生成
首先我们来回顾一下DES的子密钥生成过程:
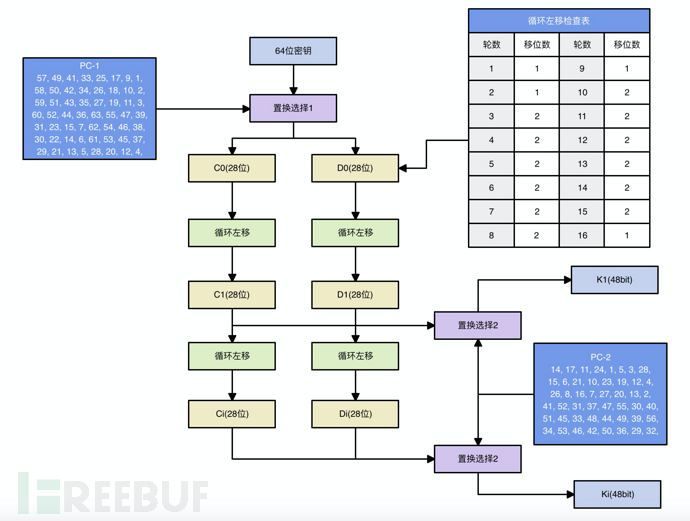
在DES加密算法中,密钥的长度为64位,但是密钥字符的每个二进制第八位设置为奇偶校验位,因此密钥的实际长度为56位。DES加密共执行16次迭代,每次迭代过程的数据长度为48位,因此需要16个48位的子密钥来进行加密,生成子密钥的过程如下:
举例说明:
密钥 K = 0001001100110100010101110111100110011011101111001101111111110001
需经过PC-1表置换,即执行置换选择1过程,PC-1表为8行7列的表,密钥K经PC-1后变为56位数据K':
K'(56位)= 11110000110011001010101011110101010101100110011110001111
取K'的前28位作为C0,则有
C0(28位)= 1111000011001100101010101111
取K'的后28位作为D0,则有
D0(28位)= 0101010101100110011110001111
获得C0,D0后进行左移操作需要查询移动位数表后得知左移位数为1。
C0左移1位为C1:
C1(28位) = 1110000110011001010101011111
D0左移1位为D1:
D1(28位) = 1010101011001100111100011110
将C1和D1合并后,经过PC-2表置换得到子密钥K1,PC-2表中去除了第9,18,22,25,35,38,43,54位。由于PC-2表为6*8的表,经PC-2置换后的数据为48位,置换后得到密钥K1:
K1(48位)= 000110110000001011101111111111000111000001110010
3.DES 子密钥逆推
根据题目条件,我们得到的是16轮子密钥Ki(Ci+Di)。
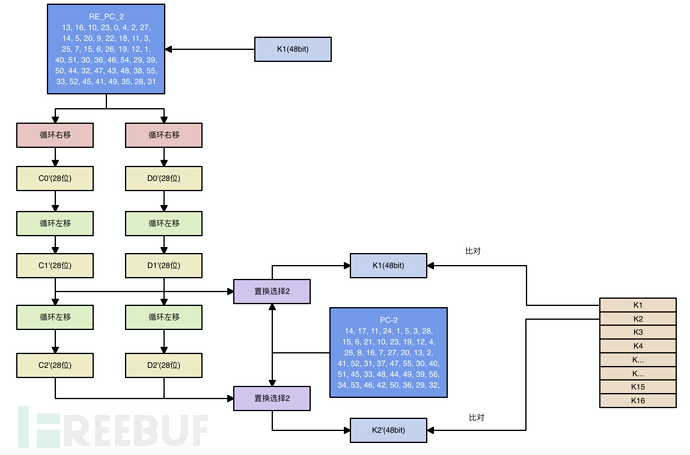
我们首先对Ki使用逆PC_2盒,得到带未知变量的netss(56比特的C+D)
代码如下:
def ReSubstitution_PC_2_Box(keyfield, sub): newkeyfield = ['*'] * 56 for i in range(len(sub)): newkeyfield[sub[i]] = keyfield[i] newkeyfield = ''.join(newkeyfield) return newkeyfield
接着对C,D进行循环右移一位,还原netss:
C, D = netss[:28], netss[28:] C = C[-1:] + C[:-1] D = D[-1:] + D[:-1] netss = C + D
使用netss生成带未知变量的十六轮子密钥:
def enkey(netss): # 生成子密钥 C, D = netss[:28], netss[28:] key = [] for i in range(16): # 十六轮子密钥生成 C, D, keyone = SubkeyGeneration(i, C, D) key.append(keyone) return key
 我们将生成带未知变量的16子密钥和题目给定的子密钥进行比对,获取真实netss:
我们将生成带未知变量的16子密钥和题目给定的子密钥进行比对,获取真实netss:
def dekey(netss): # 还原子密钥
netss = ReSubstitution_PC_2_Box(netss, RE_PC_2)
C, D = netss[:28], netss[28:]
C = C[-1:] + C[:-1]
D = D[-1:] + D[:-1]
netss = C + D
real_netss = ''
num = 0
for i in netss:
if i != '*':
real_netss += i
else:
real_netss += alphabet[num]
num += 1
keys = enkey(real_netss)
key_dic = {}
for i in range(len(keys)):
for j in range(48):
if keys[i][j] != real_key[i][j]:
key_dic[keys[i][j]] = real_key[i][j]
for i in key_dic:
real_netss = real_netss.replace(i, key_dic[i])
return real_netss
此时我们已经得到了一个不带未知变量的real_netss
00000001*11111100*110*00*000011001*01*1101*0001011000*01 00000000111111110011101000001011001001111010000101100000
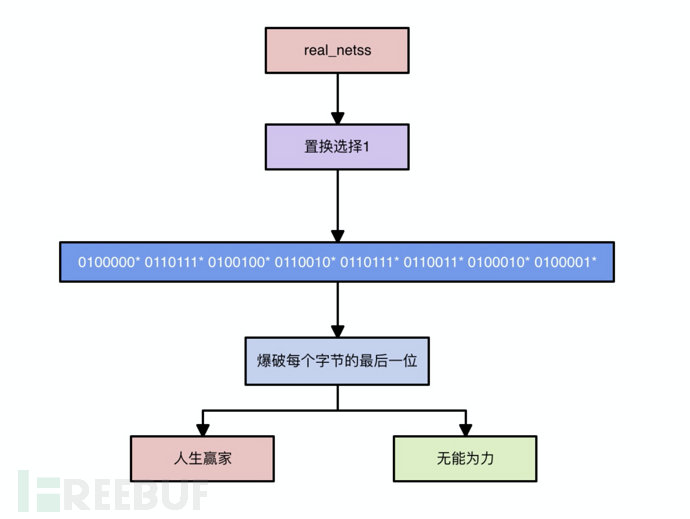 接下来要做的就是还原逆PC_1盒:
接下来要做的就是还原逆PC_1盒:
def ReSubstitution_PC_1_Box(keyfield, sub): newkeyfield = ['*'] * 64 for i in range(len(sub)): newkeyfield[sub[i]] = keyfield[i] newkeyfield = ''.join(newkeyfield) return newkeyfield
最后我们再对每个字节的最后一位进行爆破:
def BruteForce_Lowest_Bytes(key): keys = [] for i in range(8): keys.append(key[i*8:i*8+8][:-1]) for i in range(256): num = format(i, '08b') key = '' for j in range(8): key += keys[j] + num[j] print BinToStr(key),
结果:
很遗憾,我无能为力。但是可用密钥中存在anheng字样~只需要尝试三次哦。
其实,DES中第八位bit应该是奇偶校验位,但是出题人并没有将第八位bit作为奇偶校验位(也就是说我们使用奇偶校验算出来的是错的)
代码如下:
def Parity_Bit_Calculation(key): keys = [] key = '' for i in range(8): keys.append(key[i*8:i*8+8][:-1]) num = 0 for j in keys[i]: if j == '1': num += 1 if(num % 2 == 1): keys[i] += '0' else: keys[i] += '1' key += keys[i] print BinToStr(key)
结果当然是...显而易见...因为密钥在选择的时候就没有遵循奇偶校验规则,所以没有办法靠此种方法恢复密钥。
最终程序:
# -*- coding: utf-8 -*-
hexadecimalcontrast = {
'0': '0000',
'1': '0001',
'2': '0010',
'3': '0011',
'4': '0100',
'5': '0101',
'6': '0110',
'7': '0111',
'8': '1000',
'9': '1001',
'a': '1010',
'b': '1011',
'c': '1100',
'd': '1101',
'e': '1110',
'f': '1111',
}
alphabet = 'abcdefghijklmnopqrstuvwxyz'
PC_2 = [14, 17, 11, 24, 1, 5, 3, 28,
15, 6, 21, 10, 23, 19, 12, 4,
26, 8, 16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55, 30, 40,
51, 45, 33, 48, 44, 49, 39, 56,
34, 53, 46, 42, 50, 36, 29, 32, ]
PC_1 = [57, 49, 41, 33, 25, 17, 9, 1,
58, 50, 42, 34, 26, 18, 10, 2,
59, 51, 43, 35, 27, 19, 11, 3,
60, 52, 44, 36, 63, 55, 47, 39,
31, 23, 15, 7, 62, 54, 46, 38,
30, 22, 14, 6, 61, 53, 45, 37,
29, 21, 13, 5, 28, 20, 12, 4, ]
RE_PC_2 = [13, 16, 10, 23, 0, 4, 2, 27,
14, 5, 20, 9, 22, 18, 11, 3,
25, 7, 15, 6, 26, 19, 12, 1,
40, 51, 30, 36, 46, 54, 29, 39,
50, 44, 32, 47, 43, 48, 38, 55,
33, 52, 45, 41, 49, 35, 28, 31]
RE_PC_1 = [56, 48, 40, 32, 24, 16, 8, 0,
57, 49, 41, 33, 25, 17, 9, 1,
58, 50, 42, 34, 26, 18, 10, 2,
59, 51, 43, 35, 62, 54, 46, 38,
30, 22, 14, 6, 61, 53, 45, 37,
29, 21, 13, 5, 60, 52, 44, 36,
28, 20, 12, 4, 27, 19, 11, 3]
movnum = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]
def HexToBin(string):
"Convert sixteen to binary"
Binstring = ""
string = string.lower()
for i in string:
try:
Binstring += hexadecimalcontrast[i]
except:
return -1
return Binstring
def BinToStr(strbin):
"Turn the binary string to a ASCII string"
strten = ""
for i in range(len(strbin) // 8):
num = 0
test = strbin[i * 8:i * 8 + 8]
for j in range(8):
num += int(test[j]) * (2**(7 - j))
strten += chr(num)
return strten
def StrToHex(string):
"Converts a string to HEX"
hexStr = ''
for i in string:
tmp = str(hex(ord(i)))
if len(tmp) == 3:
hexStr += tmp.replace('0x', '0')
else:
hexStr += tmp.replace('0x', '')
return hexStr
def Binxor(string1, string2):
"If the length is different, only the short one is returned."
strlen = 0
xorstr = ""
if len(string1) > len(string2):
strlen = len(string2)
else:
strlen = len(string1)
for i in range(strlen):
if string1[i] == string2[i]:
xorstr += '0'
else:
xorstr += '1'
return xorstr
def SubstitutionBox(keyfield, sub): # 置换盒
newkeyfield = ''
for i in range(len(sub)):
newkeyfield += keyfield[sub[i] - 1] # watch the table
return newkeyfield
def SubkeyGeneration(freq, C, D): # 轮密钥生成函数
for i in range(movnum[freq]):
C = C[1:] + C[:1]
D = D[1:] + D[:1]
return C, D, SubstitutionBox(C + D, PC_2)
def enkey(netss): # 生成子密钥
C, D = netss[:28], netss[28:]
key = []
for i in range(16): # 十六轮子密钥生成
C, D, keyone = SubkeyGeneration(i, C, D)
key.append(keyone)
return key
def dekey(netss): # 还原子密钥
netss = ReSubstitution_PC_2_Box(netss, RE_PC_2)
C, D = netss[:28], netss[28:]
C = C[-1:] + C[:-1]
D = D[-1:] + D[:-1]
netss = C + D
real_netss = ''
num = 0
for i in netss:
if i != '*':
real_netss += i
else:
real_netss += alphabet[num]
num += 1
keys = enkey(real_netss)
key_dic = {}
for i in range(len(keys)):
for j in range(48):
if keys[i][j] != real_key[i][j]:
key_dic[keys[i][j]] = real_key[i][j]
for i in key_dic:
real_netss = real_netss.replace(i, key_dic[i])
key = ReSubstitution_PC_1_Box(real_netss, RE_PC_1)
return key
def BruteForce_Lowest_Bytes(key):
keys = []
for i in range(8):
keys.append(key[i*8:i*8+8][:-1])
for i in range(256):
num = format(i, '08b')
key = ''
for j in range(8):
key += keys[j] + num[j]
print BinToStr(key),
def Parity_Bit_Calculation(key):
keys = []
key = ''
for i in range(8):
keys.append(key[i*8:i*8+8][:-1])
num = 0
for j in keys[i]:
if j == '1':
num += 1
if(num % 2 == 1):
keys[i] += '0'
else:
keys[i] += '1'
key += keys[i]
print BinToStr(key)
def ReSubstitution_PC_1_Box(keyfield, sub):
newkeyfield = ['*'] * 64
for i in range(len(sub)):
newkeyfield[sub[i]] = keyfield[i]
newkeyfield = ''.join(newkeyfield)
return newkeyfield
def ReSubstitution_PC_2_Box(keyfield, sub):
newkeyfield = ['*'] * 56
for i in range(len(sub)):
newkeyfield[sub[i]] = keyfield[i]
newkeyfield = ''.join(newkeyfield)
return newkeyfield
real_key = ['101000001001011001000110001110110000011110011000', '111000000011011001010010100101100011011000100110', '011001001101011001110000001111000000101111100100', '110001101101000101010010000100001110100011010011', '001011101100001101010011011001111010010000010001', '001011110101000100001011101010110010010101001010', '001010110000000111011001001011001101001100000110', '000111010100100010011001010101000100010011100110',
'000111010100100111001000010000001111100101010100', '000100100110100110001101011000011010010010111000', '000110010010110100000101111010010001110000001011', '010000010010110010101101000011100101001000111110', '110100011010010010100100000101010101100111100100', '110100001000111010100010100000001000100011110001', '111100001011001000100110110000111010111000010101', '101000001011111000100110101000011001001000001011']
# real_key 存放16轮真实子密钥
K1 = real_key[0]
key = dekey(K1)
# Parity_Bit_Calculation(key) #奇偶校验
# BruteForce_Lowest_Bytes(key) #暴力破解
4.总结
通过这道CTF题目,让我更深刻的理解了DES加密原理,以前从未考虑过使用子密钥还原真实密钥。在使用最终程序的时候只需要修改real_key数组即可。在对于这道CTF题目的延伸上我们是否可以去思索如果题目只给定了16轮密钥中一轮,我们应该怎么做呢?
5.致谢
本文引用了以下文章,感谢网友的分享:
https://limbenjamin.com/articles/des-key-parity-bit-calculator.html https://stackoverflow.com/questions/7149944/how-can-i-check-the-parity-of-a-des-key https://xz.aliyun.com/t/3101#toc-4 https://crypto.stackexchange.com/questions/34199/purpose-of-des-parity-bits https://www.cxyxiaowu.com/1478.html
关注我们
Tide安全团队正式成立于2019年1月,是新潮信息旗下以互联网攻防技术研究为目标的安全团队,目前聚集了十多位专业的安全攻防技术研究人员,专注于网络攻防、Web安全、移动终端、安全开发、IoT/物联网/工控安全等方向。
想了解更多Tide安全团队,请关注团队官网: http://www.TideSec.com 或长按二维码关注公众号:






