*本文作者：GeekOnline，本文属 FreeBuf 原创奖励计划，未经许可禁止转载。

模运算，又称模算数(modular arithmetic)，是一个整数的算术系统，其中数字超过一定值后(称为模)会“卷回”到较小的数值，模运算最早是卡尔·弗里德里系·高斯在1801年出版的《算术研究》中书面公开，但在这之前模运算的方法已经深入到人类社会的方方面面，例如在时间上的运用，我国古时的《中国十二时辰图》就把一天划分为子、丑、寅、卯等十二个时辰，每个时辰相当于现在的两个小时，每过完十二个时辰又重新开始计算，这种计数方式的模就为12。

模运算在数论、群论、环论、电脑代数、密码学、计算机科学等学科中都有着广泛地应用，从奇偶数的判别到素数的判别，从模幂运算到最大公约数的求法，从孙子算经中的问题到凯撒密码问题，都充斥这模运算的身影。在密码学中，模运算是RSA及迪菲-赫尔曼(D-H)等公开密钥机密系统的基础。在电脑代数多项式分解以及多项式最大公因式、线性代数等问题，所有已知有效率的解法用到了模运算。模运算渗透了人类生活的方方面面，因此如何在当下计算系统中更加高效的运用模运算也是一个十分关键的问题，尤其在面对比较消耗资源的大数幂模运算时更应该注重此类算法的高效性。

普通幂模算法

由于模运算可以将所有中间结果和最后结果限制在一个范围内，对一个k位的模数n，任何加、减、乘、除的中间结果将不会超过2k位长，因此在计算大数幂模时通常会考虑结合模运算分解幂过程，防止计算过程产生大数中间值进而发生溢出等错误的情况，例如：

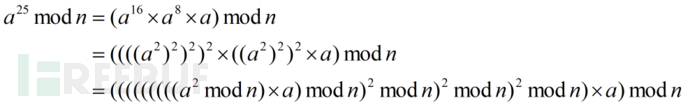
图1 普通幂模算法变换

以上优化算法使用了模运算的运算法则：

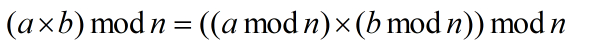
图2 乘模运算变换

这种算法称为加法链(addition chaining)，或二进制平方和乘法方法，算法的C语言描述：

利用该算法可以有效避免因为幂运算产生大数而使得后续模运算无法进行的问题。

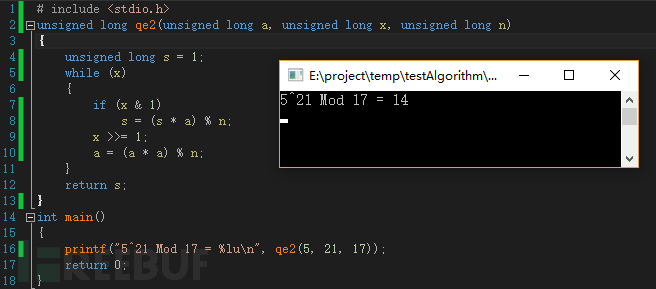
图3 程序示例计算简单幂模

图4 计算器验证程序正确性

当计算一些高次幂模时，普通计算器由于按顺序计算，在幂运算时产生大数导致后续无法进行，而加法链操作则由于分解了幂运算，使得每次的中间过程变量都限制在了模范围内，因此可以计算更加复杂的幂模运算。

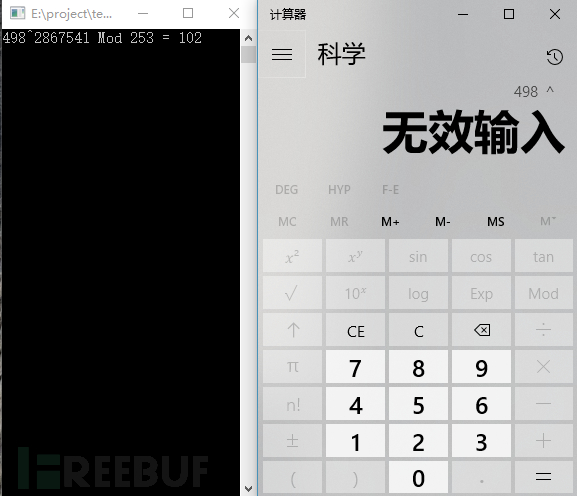
图5 计算器程序在计算486^2867541时产生大数导致错误

反汇编上述算法后，发现虽然该算法有效的解决了幂模过程中幂运算产生大数的问题，但在实际计算模运算时仍旧采用了除法指令，且采用除法指令的次数和幂运算的指数正相关，而我们知道在计算机系统除法指令是一个相当耗时的指令，因此该算法不能算作一个高效的幂模算法。

图6 加法链算法反汇编

Montgomery算法

Montgomery算法由1985年美国数学家Peter L.Montgomery在其论文"Modular Multiplication Without Trial Division"中向大家展示如何在不使用除法的情况下实现快速乘模计算，下面便以此种算法介绍高效幂模算法的实现。

首先考虑最初的我们进行模运算的基本方法，通常最容易回想起的就是使用除法然后得到余数就是我们要取的模(此处只考虑正整数运算)，即：

图7 常规模运算公式

现在我们知道如果利用此公式在计算机中不可避免的将使用除法进行运算，于是在大型幂模计算时是不可取的，那么我们考虑一种更原始的计算模的运算——减法：

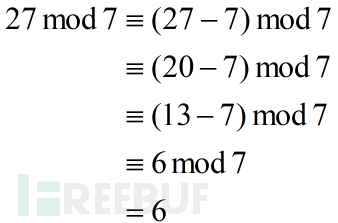
图8 使用减法的思想计算模

使用该思想有效的避免了在模运算中使用除法指令，但是当计算的数非常大时，这种运算将进行太多次循环减法，可以想象在该数达到某一个界限时使用减法进行模运算的资源消耗将和除法相差不大，当超越这个界限那么减法思想的求模运算几乎是毫无意义。在排除了减法和除法后，我们转而考察使用加法进行模运算的可能性，这也是Montgomery算法所探寻的方向，我们用例子来体会这种思维转变的路线。

考虑计算 43*56 (mod 97)，因为给出的两个数值并不是很大，可以很快计算出乘积43*56=2408，此时可以使用除法较快的计算出模的结果，也可以使用减法得出结果，但我们此时不考虑计算模，而是使用乘积加上n倍模数97使得该乘积(2408)转变成我们人思维中好计算的数字，比如数字低位全为0的状态：

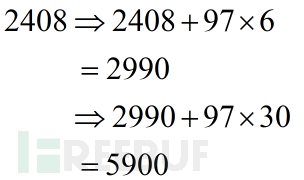
图9 经过两次变换后的乘积表示

那么此时如果再让我们计算5900 / 100，那么对于我们人脑来说这再简单不过了，可以瞬间口算出结果为59。可惜的是，59并不是我们要求的43*56 mod 97的结果，但我们确实认清了在此时如果除数是100而不是97，那么我们的计算会轻松很多。

那么既然在我们已认知的世界中没有这种理想的计算环境，那么我们就考虑制造一个，这种思维与传统的数学思维非常相似：比如当笛卡尔坐标系无法帮助我们有效建模时，我们便会考虑采用极坐标系去建模；当时域信息无法进行有效分析时，我们便会考虑转换至频域进行分析。在某一个域类无法解决的问题到另一个域类可能就是1+1=2的难度。Montgomery算法就建立了这么一个空间，在普通计算域的除数97，转换到Montgomery域中除数就变成了100，因此对于模运算的难度会陡然下降。

用以上例子(43*65 mod 97)介绍Montgomery域，常规世界的数字形式需要转换成Montgomery域中的数字形式，首先我们的模数为97，这是一个2位的十进制数，那么计算Montgomery域中第一个关键变量R，使得：

图10 计算Montgomery域变量R

在当前例子中模数为97，b为10，计算得出m=2，R=100。另一个关键变换针对两个乘积因子：

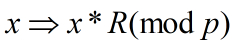
图11 乘数因子Montgomery表示

当前例子中的乘数43的Montgomery表示法为43*100(mod 97)=32。当然到现在我们还看不到这种变换有啥意义，貌似除了增加计算量之外并没有给后续的计算带来什么方便，我们接着看后续的变换。考虑以下计算：

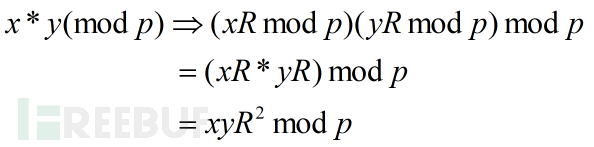
图12 计算x*y(mod p)在Montgomery域的等价表达式

但在大数乘模运算中，通常我们希望中间结果仍然保留在Montgomery域中，因为后续还有很多乘法操作需要进行，在此时直接将结果表示为现实域结果将导致很大的中间转换开销且并不符合我们的意愿，因此我们实际希望在Montgomery域中计算x*y*R(mod p)，也就是现实域中的x*y。所以在Montgomery域中每次计算两个因子的乘积后需要除以R，调整参数后的结果才是x*y在Montgomery域中的中间结果。

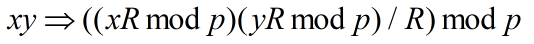
图13 x*y在Montgomery域中的计算结果

在本次列举的实例中(43*65 mod 97)即是中间乘积的结果除以R=100。以实例解释上述推导：

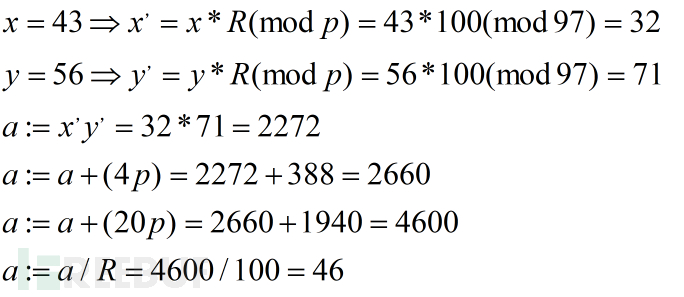
图14 计算x*y的实例

其中

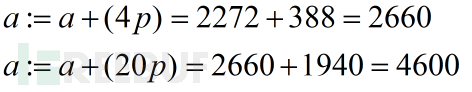
图15 Montgomery域中形式变换

基于一个数学事实：

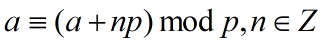
图16 Montgomery域变换中的数学原理

在上述例子中我们计算出一个在Montgomery域中xy(mod p)的结果46，对应现实域的x*y*R(mod p)，因此结果必然不是现实域中(43*65 mod 97)的结果，需要经过逆变换后才能代表现实域的结果，变换公式为：

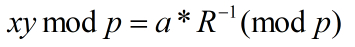
图17 Montgomery域结果转换成现实域结果

其中：

图18 R^-1的计算方法

因此将实例中的结果转换后得到结果：

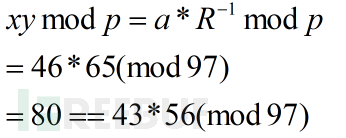
图19 验证转换后的结果是否符合计算结果

我们发现此算法的特点是在算法首端会将现实域的数字转换成Montgomery域中的表达形式，在Montgomery域进行整个求解过程后再将Montgomery域中的结果转换成现实域中的结果，从而完成整个计算，其中巧妙之处在于Montgomery域的创建使我们需要进行2272/97运算变成了4600/100的运算，因此加快了我们人脑的运算，其在转换过程中的计算则又加大了我们的运算量，但考虑幂模的形式a*a*a*a....*a(mod p)的进行中所消耗的运算量，则这两次转换的计算量其实并不算什么。上述思维也就是Montgomery论文中提及的第一个约简算法：

图20 摘自Montgomery论文

其中为了将不好运算的2272转换成4600格式，采用了(T mod R)N' mod R公式来实现，其中N'满足图18的公式，可以用扩展欧几里得算法求得，将上述思想转换成C语言格式：

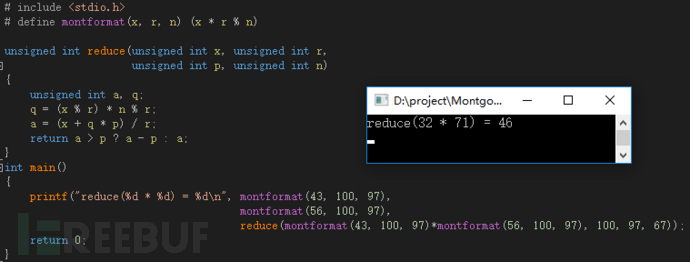
图21 Montgomery REDC函数C语言

其中C语言中reduce函数中n=67即是上面提到的N’变量，可以用扩展欧几里得算法得到：

图22 扩展欧几里得求N‘变量

我可以反汇编调试该代码看看计算机到底怎么思考这段代码，可以看到计算机思考这段代码非常艰难，我们眼中的4600/100，它完全无法理解，以至于它最后还是选择了用除法解决问题，而我们人脑面对这个算式时几乎不用除法，通常的做法都是"抹零"操作，我们可以用一种更书面一点的描述，4600/100时我们其实对被除数进行了移位操作，后面的除数是100，因此我们决定将4600右移两位最终得到了46。而计算机无法体会这种思维，因为4600对于它来说就如图24一样，他没法进行"抹零"操作完成运算。

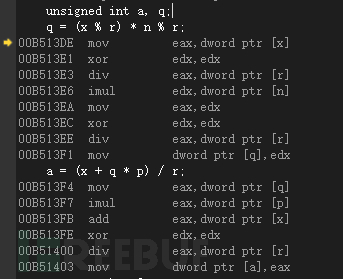
图23 反汇编关键代码处

图24 计算机思维中的4600

对于人脑来说大家习惯了10进制的计算世界，看待4600/100非常简单，但在计算机的世界它们并不喜欢十进制，而是更喜欢二进制的计算方式，因此Montgomery域中用于简化计算的R值针对人类思维模式是10^m，而针对计算机的思维模式就是2^n。因此在变换中应该使用R=2^7=128>97进行变换操作，以R=128对上述实例计算进行变换，带入C语言程序中：

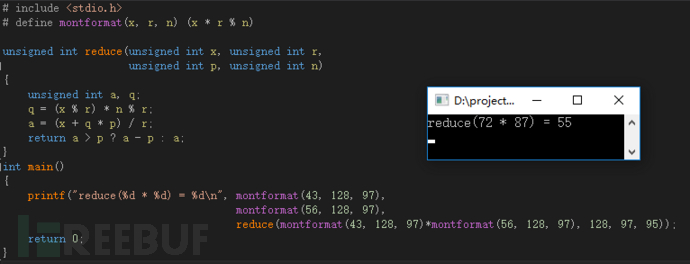
图25 以R=128对实例计算进行变换

图26 计算此时的N‘变量

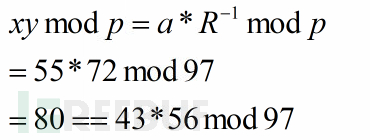
图27 将Montgomery域结果转换成真实域结果

此时的我们在Montgomery域中产生了机器非常喜欢的结果7040(72*87 + (72*87)mod128 * 95 mod128 * 97)，机器在这时就可以模拟人类的处理方法使用"抹零"操作快速完成除法运算，抹掉后续的零后机器得到了110111的结果，换算成我们青睐的10进制也就是55，再用Montgomery逆变换将结果转回现实域即得到真实的运算结果。

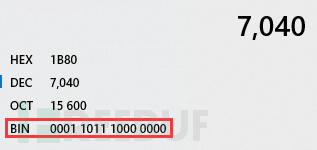
图28 Montgomery域中机器青睐的结果

所以根据机器对待这种算法的方式我们优化C语言代码，经过优化后我们将传递给我们的关键函数以m值(即R=2^m中的m)而不是直接将R值传递进去，那么内部我们的关于取模和除法函数全以&和>>运算取代，通过关键函数的反汇编可以与之前图23进行对比，里面的除法指令div已经全部消失，实现了不使用除法而进行模计算的目标，且我们依旧得到了我们想要的结果。此代码得到了有效的改善，且当在大数幂模计算时性能上的优势会随着运算量的增大而进一步凸显出来。

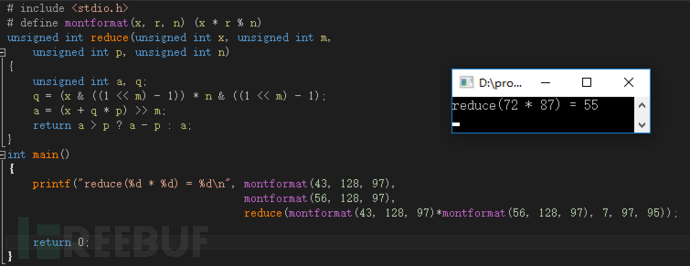
图29 针对机器思维优化的代码

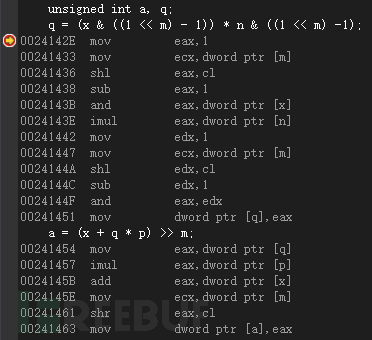
图30 优化代码的反汇编

结合加法链的思想在这里我们就可以完成一个简单版本的Montgomery快速幂模C语言程序，其中ExtBinEuclid函数为扩展欧几里得算法，在此不再进一步做深入探究：

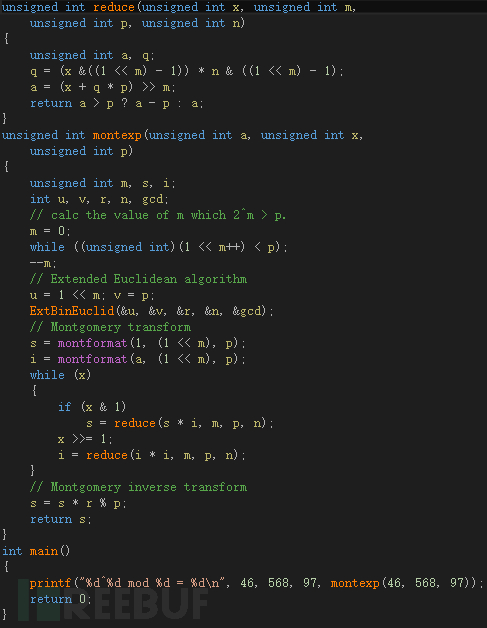
图31 结合加法链思想的Montgomery幂模程序

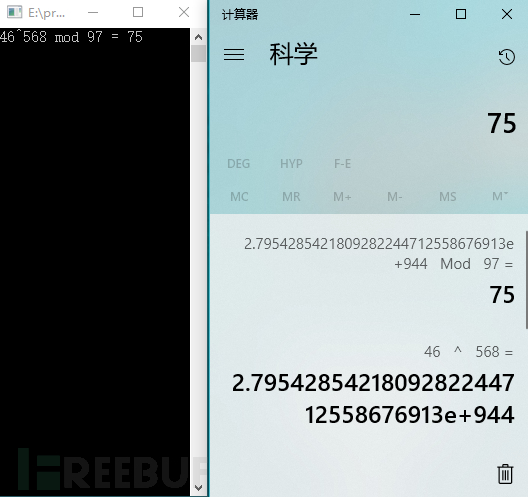
图32 验证程序计算的正确性

通过完成的程序我们可以发现相比普通的加法链算法，Montgomery算法多了一些预计算，包括进入Montgomery域前对现实域中数字的转换，以及计算完成后，对Montgomery域结果再次转换到现实域中，这里包含了三个除法指令，再考虑使用扩展欧几里得算法计算一些运算中需要使用的变量，可以看出在此算法中除法指令为有限常数，在Montgomery域的循环计算中不包含任何除法指令，因此该算法比普通的加法链操作更加高效，当应对大数的幂模计算时，由于普通的求模公式将不可避免的使用大数除法操作导致性能成倍降低，而Montgomery算法由于其不存在大数除法的问题，因此其仍然能保持良好的性能。

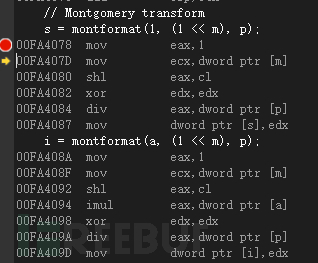
图33 进入Montgomery域前的变换

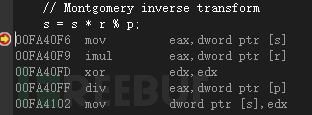
图34 离开Montgomery域的逆变换

小结

在现今软硬件高速发展的时代，很多人都会有疑问“算法还重要吗？”，其实永远不会有太快的计算机，因为人们总是会想出新的应用，虽然如今的计算机计算能力每年都在飞速增长，成本也在不断降低，但我们所面临的数据量也是呈指数级的增长，每个人每天都会创造出大量的数据(照片，视频，语音，文本等等），如何更快更有效的处理这些数据这成了各个领域亟待解决的问题，在未来不论是三维图形，大数据处理，机器学习，语音识别等都需要更加卓越的算法来解决问题，因此算法的重要性将随着人类生活水平的提高而处于日益加强的状态。

*本文作者：GeekOnline，本文属 FreeBuf 原创奖励计划，未经许可禁止转载。