本文涉及知识点实操练习：CTF从入门到实践-CTF一站式学习平台-合天网安实验室

前言：

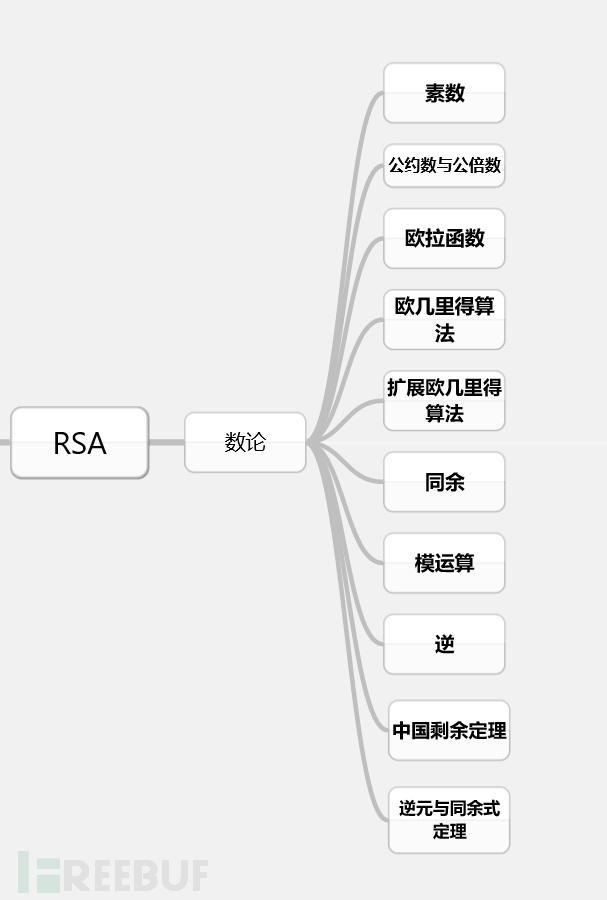
在CTF的密码题目中，RSA以其加密算法之多且应用之广泛，所以在比赛中是最常见的题目。学习密码学并不难，但首先得打好数学基础，并在攻破密码的学习之路上持之以恒。今天我们就来打开RSA加密世界的第一扇门<数论>。

数论基础：

1.素数

2.公约数与公倍数

3.欧拉函数

4.欧几里得算法

5.扩展欧几里得算法

6.同余

7.模运算

8.逆

9.中国剩余定理

10.逆元与同余式定理

1.素数：

定义：

一个大于1的自然数，除了1和它本身外，不能被其他自然数整除（除0以外）的数称之为素数（质数）；否则称为合数。

如：

3×4 = 12,不是素数。

11除了等于11×1以外，不能表示为其它任何两个整数的乘积，所以11是一个素数。

关于素数有以下事实：

（1）如果p是素数，且p | ab（表示ab能被p整除），则p | a或 p | b ,即p 至少整除a与b中的一个。

（2）（算术基本定理）每个整数n ≥ 2 ,均可分解成素数幂之积：

n =

若不计因数的顺序，这个分解式是唯一的。其中k ≥ 1，(1 i ≤ k)是两两互不相同的素数，(1 i ≤ k)是正整数。

（3）素数有无穷多个。

2.最大公约数与最小公倍数

定义1：

设，是两个整数。如果 d | 且 d | ，那么d就称为是和的公约数（或公因数）我们把和的公约数中最大的称为和的最大公约数，记作gcd(,).

当gcd(,) = 1时，我们称和是互素的。

定义2：

设，是两个整数。如果 | 且 | ，那么 就称为是和的公倍数。我们把和的正的公倍数中的最小的称为和的最小公倍数，记作。

3.欧拉函数

定义：

对正整数n，欧拉函数是小于或等于n 的数中与n 互质的数的个数，

记作：φ(n)。

例如：φ(8) = 4 ,因为1，3，5，7均与8互质。

性质：

(1) 若 n 为一素数 P，则：φ(P) = P-1

(2) 如果P是素数，k≥则：φ() = (P-1)×

例如 ：求φ(16)，由于 16 = 2×2×2×2，故φ(16) = (2-1) × = 8

(3) 若 n 为任意两个互质的 数a,b的积，则：φ(a*b) = φ(a) × φ(b)

例：求φ(40)，由于40 = 5×8，所以φ(40) = φ(5) × φ(8) = 4×4 = 1

(4)对于整数n≥2，根据算术基本定理，n可以分解成唯一的形如 n=的分解式，则：φ(n)=n(1-)(1-)…(1-)

4.欧几里得(Euclid)算法

欧几里得算法又称为辗转相除法，用于求两个数的最大公约数。

原理：GCD(x,y) = GCD(y，x mod y) ，x>y

1.python代码实现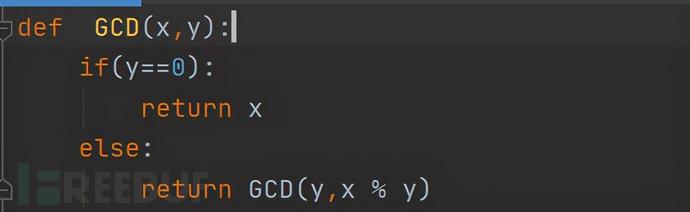

2.python第三方库：

gmpy2.gcd(a,b) #求a,b的最大公约数

Crypto.Util.number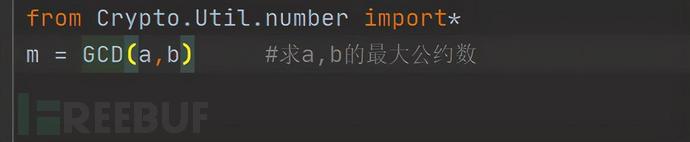

5.扩展欧几里得算法

定义：

在已知x，y时，求解一组解a,b，使得ax+by = GCD(x，y)

算法输入：两个正整数x和y

算法输出：x和y的最大公因数gcd(x,y)及满足等式ax+by=gcd(x,y)的整数a和b

python代码实现:

gmpy2库函数gcdext()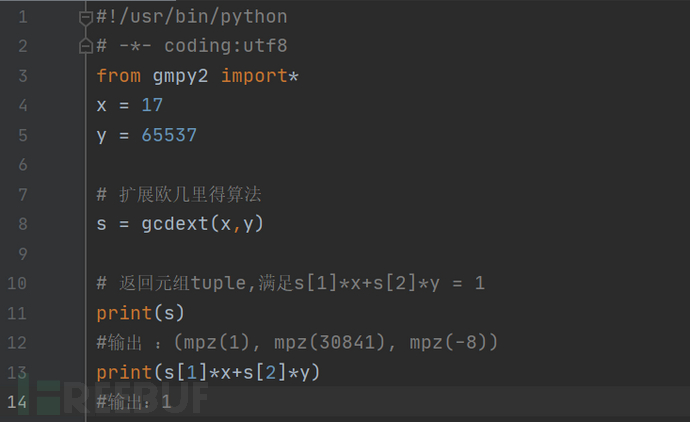

6.同余

定义：

设a,b是整数，n≠0，如果n|(a-b)，则称a和b模n同余，记为a≡b(mod n)，整数n称为模数。

由于n|(a-b) 等价于 -n|(a-b)，所以a≡b(mod n) 与 a≡b(mod (-n))等价。因此，一般我们总假定模数n≥1。

同余的性质

性质1：

1. 自反性：a ≡ a (mod m)

2. 对称性：a ≡ b (mod m)，↔b ≡ c (mod m) ↔a ≡ c (mod m)

性质2：

(1)若a ≡ b (mod m)，c ≡ d (mod m)

则：a±c ≡ b±d (mod m)，ac ≡ bd (mod m)

特别的，对于一个整数e,都有a±e ≡ b±e (mod m)，ae ≡ be (mod m)

(2)若a ≡ b (mod m)，k>0，则ak ≡ bk (mod mk)

(3)若a ≡ b (mod m)，d是a，b的公因数，则 ≡

(4)若a ≡ b (mod m)，d|m，d>0，则: a ≡ b (mod d)

(5)若a ≡ b (mod m)，则:

(6)(a×b)mod m = (a mod m ×b mod m )mod m

(7)mod m = mod m

7.模运算

定义：

a模n的运算给出了a对模n的余数，这种运算称为模运算。注意：模运算的结果是从0到n-1的一个整数。

模运算就像普通的运算一样，它是可交换、可结合、可分配的。而且，对每一个中间结果进行模m运算后再进行模m运算，其作用与先进行全部运算，然后再进行模m运算所得到的结果是一样的。例如：

(a+b)mod m=((a mod m)+(b mod m)) mod m

(a-b)mod m=((a mod m)-(b mod m)) mod m

(a×b)mod m=((a mod m) ×(b mod m)) mod m

(a×(b+c))mod m=((a×b) mod m+(a×c) mod m) mod m

这些性质对于密码学中的数学计算非常的重要，模运算可以将所有中间结果和最后结果限制在一个范围内。对于一个k位的模数n，任何、加、减、乘的中间结果将不会超过2k位长，这样避免了巨大的中间结果，使得计算机能够有效的处理数据。

如：计算(mod n)，不要直接进行7次乘法和一个大数的模运算：

(a×a×a×a×a×a×a×a)mod n

相反，应该进行三次比较小的乘法和三次比较小的模化简：

这样就可以避免巨大的中间结果出现。

8.逆

定义：

若m≥1，gcd(a,m)=1,则存在c使得：

ca≡1(mod m)

我们把c称为a对模n的逆，记作，在模数已经指明的情况下，有时也记作。

在(a,m)=1时，我们可以使用扩展欧几里得算法来求a的逆元：，这是因为：扩展欧几里得算法可以找到整数x,y使得ax+my=1，这样

9.中国剩余定理

中国剩余定理（Chinese remainder theorem，CRT），又称孙子定理，最早可见于中国南北朝时期（公元5世纪）的数学著作《孙子算经》中，为一次同余方程组的起源。

定理(CRT):

设,……,是两两互素的正整数，M=…,

=(i=1,2,…,k),则同余方程组：

有唯一解: x=(mod M)

其中≡1(mod )，i=1,2,…,k

代码实现：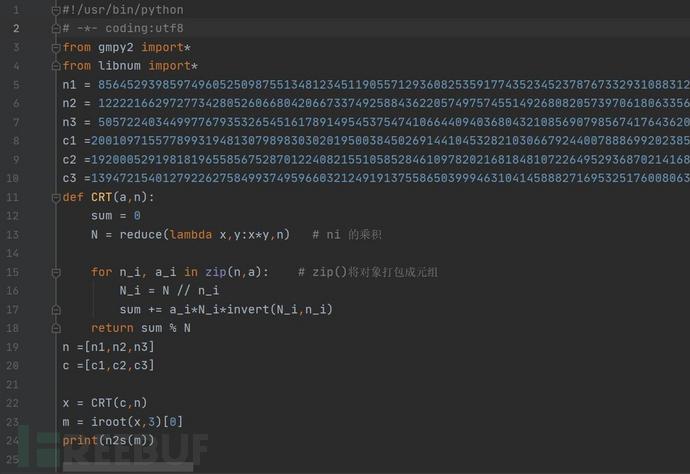

10.逆元与同余式定理

1模运算重要公式：

(a+b) % m = (a % m + b % m) % m

(a-b) % m = (a % m - b % m) % m

(a*b) % m = (a % m * b % m) % m

% m = % m

2威尔逊定理： (wilson’s theorem)

若p为素数，则：(p-1)!≡-1(mod p)⟹推导：(p-2)!≡1(mod p);

其逆定理同样成立。即：若(p-1)!≡-1(mod p) ,则p为素数

3二次探测定理：

定义：

若p是素数且 0<x<p,则 ≡1(mod p)仅有的两个解为：x=1或x=p-1

证明：由于≡1(mod p)，所以：-1≡0(mod p)，即(x+1)(x-1)≡0(mod p)

4费马小定理(Fermat)：

若a为正整数，P是一质数，则：GCD(a,p)=1

那么，推论:

，推论:=a mod p

5欧拉定理(Euler)：

若a与m互质，则：

后记：

数论基础的知识点比较杂乱繁多，这篇文章写的时候尽可能的去精简了，其中的定理及公式是必须要牢记于心的，后面的RSA加密算法的讲述中我会介绍定理及公式在RSA中的应用。

学习完数论基础后，后面我们将开始学习RSA的常见攻击算法及加密原理，以及各种工具的使用和python第三方库的函数调用。

本文首发于“合天智汇”公众号 作者：CNinja