引言

“这横贯数千年的西法史，说来说去就是讲这么一个问题。”，老师转过身，在黑板上写下了几个单词，“What is ___?”。一位女同学在台下脱口而出，“law”。老师把粉笔一丢，挥挥手，微笑示意着我们下课。毫无疑问这是一堂精彩绝伦的法律课，但身为信安专业的学子，自然而然萌生了另一个想法：黑板上的填空，如果替换成 security，该作何解答？

时光倒回数年前，记得在马云的访谈录上，见过这么一句话“做淘宝，最难的是建立诚信体系”。当时尚小不能理解，现在有所感悟。连萍水都未曾相逢的买家与卖家，凭什么信任“买家是真的买家，卖家又是真的卖家”，凭什么能够实现”一手交钱，一手交货“？淘宝的解决思路是：淘宝作为可信第三方介入交易，在买家下单后，先将货款转入到淘宝的指定账号，只有在买家确认收货后，卖家才能从淘宝收到相应的货款。问题进一步延伸，淘宝凭什么能够成为可信第三方？成为可信第三方后，又是如何分发和管理其数字证书，确保互联网上每一笔交易的顺利进行？

回答上述两个问题都离不开建立一套安全体制，但相比于安全体制如何建立，更为重要的一点是，究竟如何去理解“安全”，即回答“What is security?”。

密码学大牛 Bruce Schniner 在其著作 Applied cryptography : protocols, algorithms, and source code in C提到了安全的定义，笔者认为非常恰当，援引如下：

如果把一封信锁在保险柜中，把保险柜藏在纽约的某个地方，然后告诉你去看这封信，这并不是安全，而是隐藏。

相反，如果把一封信锁在保险柜中，然后把保险柜及其设计规范和许多同样的保险柜给你，以便你和世界上最好的开保险柜的专家能够研究锁的装置，而你还是无法打开保险柜去读这封信，这才是安全的概念。

为了更好地理解什么是安全，可行的方案是学习信息安全领域的道统学科——密码学。

密码学

密码学是为了达到机密信息不被非授权地获知的目的,而采取的某种手段或方式，主要基于数学或物理的某种变换来实现加密/ 解密。密码学的研究对象可以抽象为一个四元组：（明文，密钥，密文，加解密算法），即研究 p = D_k(E_k(p)) 的实现 。

历史

密码学是一门古老的学科，在数千年前已经诞生，并且得到广泛应用：

• 与密码学 cryptography 意思相近的一个单词是 cryptology，在古希腊文中的意思是“如何秘密地书写单词”。440 B.C. 古希腊战争中，奴隶主赫斯坦为推翻波斯人统治，想与爱奥尼亚城统治者联合行动，采用了“隐写术”进行保密通信。他剃光一位忠实奴隶的头发，将情报刺在其头皮上，等待头发长出来之后，就让奴隶出发前往爱奥尼亚城。奴隶到达目的地后，让人剃光自己的头发，对方就看到了奴隶头皮上刺的情报。

• 现代的门限共享方案，早在我国周代就有其雏形。据史料记载，周代的著名军事家姜尚（字子牙）发明了“阴符”和“阴书”。其中，阴书采用“一合而再离，三发而一知”的方法，将一份军事情报分成三份，分别放在三枚竹简上，派三名信使各持一个竹简出发，到达目的地后，三枚竹简再合而为一，就可得知军事信息的原意。

除了上述两个例子，诸如藏头诗、卡丹网格式密码、二战期间周恩来总理发明的“豪密”、让日本摸不着头脑的“纳瓦霍密码”，也都是密码学的实际应用。然而这些历史应用可能离当下生活仍旧太遥远，因此不妨移目下方这个小故事：

在百度的密码吧里，这则已有 20118 个跟贴，名字为《求救，我已经快想爆了》的帖子里，发帖主人 HighnessC 说：“最近和一个心仪的女生告白，谁知道她给了一个摩斯密码给我，说解出来才答应和我约会。可是我用尽了所有方法都解不开这个密码。。好郁闷啊。只能求救你们了。”

<省略解密过程>

吧友们最后直呼，“祝楼主幸福咯。因为她是爱你的！！”

故事的来龙去脉，可上知乎获悉：https://www.zhihu.com/question/20011317/answer/728551774。

对称加密与非对称加密

言归正传，回到密码学理论本身。无论是古典密码学，还是现代密码学，基本的加密模式都是分组加密（流密码可以视为分组长度为 1 的分组加密）。分组加密最本质的要求是 Claude Shannon 提出的扩散（Diffusion）和混乱（Confusion），它们分别基于换位和替换操作实现。换位和替换即常说的的 S-box(Substitution) 和 P-box(Permutation)。S-box 将输入的数据块映射为另一个数据块，例如将字母"A"替换为"X"。P-box 则是将输入的数据块按照预定的规则重新排列，例如将字符串"ABCD"重排为"CDAB"。运用 S-box 和 P-box 的示例比比皆是，例如耳熟能详的 Caesar cipher 和 Vigenere cipher（图 1、2 分别是 Caesar，Vigenere 的图示）。

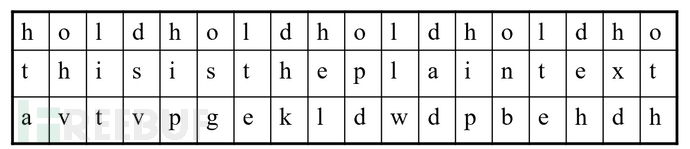
然而基于线性变换的 S-box 与 P-box 难以抵御词频统计等攻击。现代密码学中，加解密算法的安全性不再依赖于线性变换，而主要依赖于某种非线性变换，加解密算法的原型也往往基于某类数学难题，像基于大数因子分解难题的 RSA、基于离散对数难题的 DH 和 DSA、基于椭圆曲线离散对数难题的 ECC。

以上讨论的密码学大多属于对称加密的范畴，对称加密的特点是加密与解密过程中使用的密钥是相同的，既然要用到相同的密钥，首当其冲的问题就是通信双方如何协商这一密钥？即如何解决通信双方的密钥分发问题。为讨论密钥分发问题，不妨先建立一个通信模型：

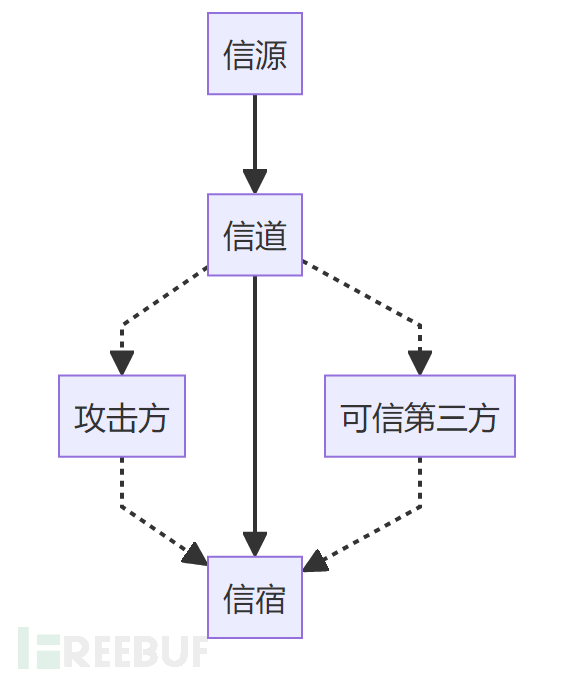
具体考虑"首次通信"和"不安全信道通信"这两种场景，对于从未通信过的发送方和接收方，双发无法确认对方的身份，无法事先共享密钥，难以进行首次通信；在不安全信道中交换密钥存在风险，密钥可能被窃听或截获。一旦密钥泄露，攻击方就可以解密通信内容，进而窃取、篡改、伪造通信内容。综上，不难发觉对称加密难以解决密钥分发问题，而且对称加密还存在以下缺陷：

1. 无法实现不可否认性（抗抵赖性）。设想某机密信息被泄露，通信的发送方和接收方都有可能是泄密者，若第三方介入尝试取证，就会遇到无法唯一确认泄密者身份的问题。

2. 密钥管理负担重，每对通信双方都需要一个唯一密钥，随着通信参与方数量的增加，密钥数量以 N^2 规模增长。

在对称加密面临以上问题的情况下，非对称加密的出现填补了这些缺陷。1976年，Whitfield Diffie 和 Martin E. Hellman 发表了一篇极其重要的论文—— New Directions in Cryptography，开创了非对称加密体系（公钥加密体系），二人因此荣获 2015年 图灵奖。这一体系的关键在于使用一对公私钥，其中公钥用于加密，私钥用于解密。这种机制允许通信实体在不事先共享密钥的情况下进行安全通信，从而解决了对称加密在首次通信和不安全信道通信中的局限性。关于非对称加密的模式，可以举一个简单的例子加以说明（以下 c 代表密文，p 代表明文）：

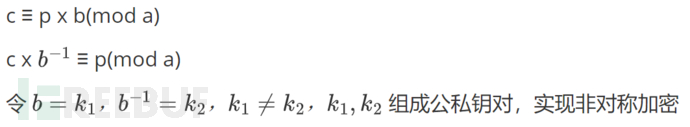
值得一提的是，DH 二位虽然提出了非对称加密体系，但并没有给出一个实例，因为找到一个单项陷门函数并非易事。读者可能会好奇什么是单项陷门函数？单项陷门函数是非对称加密体系的基础，单项函数好理解，即从一方向计算容易，从另一方向反推很困难的函数，如 Hash 函数。陷门函数是一种在一个方向上很容易计算，但在没有特殊信息的情况下很难在相反方向上计算（寻找它的逆）的函数，称为“陷门”。陷门函数是单向函数的一种特殊情况。单向陷门函数的特点概况如下：

在1979年，Ron Rivest, Adi Shamir 和 Leonard Adleman 发明了 RSA算法，将非对称加密正式带入人世间，三位作者也因此共同分享 2002年图灵奖。非对称加密有很多应用场景，PGP（Pretty Good Privacy）是其中一种。PGP 用于保护电子邮件通信的隐私和安全性，其应用过程的一种数学表达式如下：

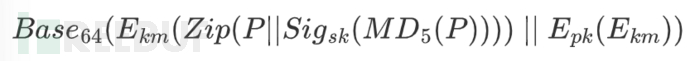
具体流程：首先用单向函数生成明文 P 的摘要（用于后续消息完整性验证），再用私钥 sk 签名摘要（用于后续消息来源验证），而后将签名与摘要压缩（提高传输效率）。为了防止攻击者窃取，用对称密钥 km 加密压缩后的消息，并用接收方的公钥加密 km，最后采用某种编码方式，将消息编码后发送给接收方。接收方收到消息后，按照上述过程的逆过程进行解密。以下是一个 PGP 脚本 demo。

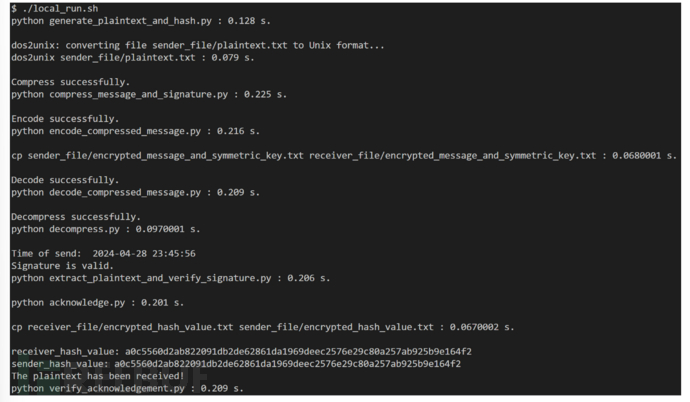
关于 PGP 的具体实现，可参考：https://github.com/955xiaoSu/Trusted-transmission-based-on-PGP。

以上从密码学的角度讨论了“What is security?”，以下笔者将从计算的角度进一步分享对这个问题的理解。

计算上不可行

从广义上，笔者认为“安全等价于计算上不可行”。为了探讨“计算上不可行”这个概念，不妨先聊聊计算这件事。

计算是什么？对于 CS 行业的我们，第一反应可能是，计算机在做的事情是计算！而后开始联想冯诺依曼计算机体系的计算流程，即有一个输入设备读取输入，其次有存算设备来处理中间结果，最后输出设备展示计算结果。

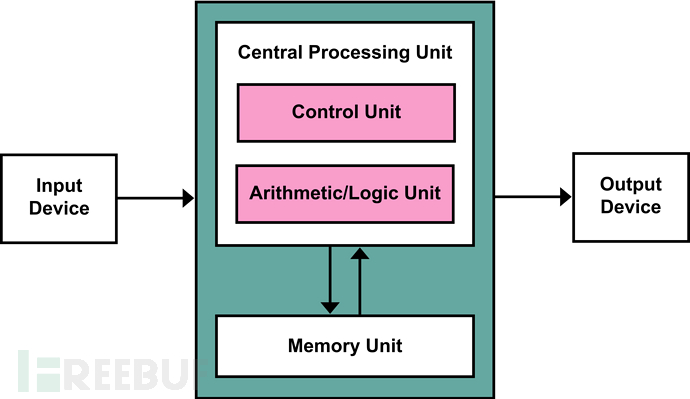
但除此之外，还有没有别的计算场景呢？

• 玩剪刀石头布是不是计算？

• 用笔在纸上做做算术、几何是不是计算？

• 拿起眼前的水杯喝水是不是计算？

在以上这些场景，人类大脑都需要进行时空方面的计算，确定肌肉的紧张程度，实现在特定的时空完成特定的动作。笔者认为在本质上，”计算”是一种”映射“，是对输入的响应，响应体现为输出，所以计算可以用如下范式表达。

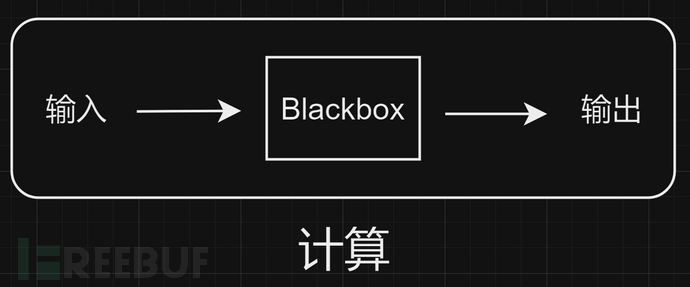
运用上述范式解释“睡眠”这一行为，首先将人体的感官与皮肤抽象为一个传感器，用于接收现实世界的输入（如光线、声音）。当夜幕降临，人体在生物钟的控制下，开始释放褪黑素、腺苷等化学物质，提升睡眠压力，让人体感到困倦，此外，人体接收到的各路信息（如昏暗的光线）也会提示到点了该上床睡觉了。与此同时，下丘脑作为大脑皮层的门卫，会控制相应的信号进入皮层促进睡眠，同时屏蔽一些不利于睡眠的信号。当心率、体温等指标都被调整到合适的范围时，人体逐渐进入睡眠状态。在睡眠场景下，“Blackbox”是人体神经信号的处理与传导，输出是人体呈现出睡着的状态（很明显的特征是肌无力）。

聊完计算之后，可以接着探讨“计算上不可行”。笔者认为，“计算上不可行”有两层基本的含义：

1. 不可计算。通俗点儿说就是做不到，包括但不限于以下两种情形：计算消耗的资源超过人类所能获取的极限、问题目前无法计算。
   前者好理解，计算需要消耗能量，根据能量守恒定律，能量是不可能凭空产生的，因此计算所消耗的能量客观上不能超过人类所能使用的能量极限；对于后者，目前通用计算机的模型是图灵机，图灵机被希尔伯特形式系统所定义，而哥德尔证明了希尔伯特形式系统是不完备的！这意味着计算机的能力存在着上界，也说明人类认知能力存在上界，上界之上的世界是目前无法理解也无法计算的。

2. 可计算但不值得，换句话说即计算代价过高。道哥在《计算》中提到这么一个观点：

计算与安全是一枚硬币的两面，安全是由计算强度保证的。

深以为然。因为世界上不存在绝对安全的系统，安全追求的并不应该是所谓万无一失的系统，而应该着眼于提高攻击者的计算强度。例如让攻击者为追求 ￥1 价值的目标，付出至少 ￥2 的代价；又或者设计一个方案，让攻击者破解保密期限只有 1day 的机密消息，至少需要花费 2day 的时间。“提高攻击者计算强度”这样一种安全方案的可行性，已经被世界所存在的单向函数所证明。世界存在单向函数的一个例子是：根据刘仁文：论死刑的成本，死囚从被判处死刑到执行花费的金额高达数百甚至上千万美元，而构成死刑的犯罪成本才多少呢？

上述两个章节分别从密码学和计算的角度讨论了“What is security？”，在最后，笔者尝试从系统的角度对此问题进行总结。

系统安全

在某讲坛上，笔者有幸获得了提问道哥的机会。

”您觉得在学习安全的过程中，最重要的思维是什么？“

”系统安全。“

系统安全成为了笔者看待安全的全局出发点，从前听闻过的一系列攻击，蠕虫、震网、幽灵、熔断、西工大 TAO 攻击、CVE-2024-3094 xz 软件包后门……都被“系统安全”这根绳紧密串联在了一起，这些攻击不再是零散的，而是以树形结构被有序组织在脑海中。

在系统的视角下，考虑安全问题，可以围绕信息的生命周期进行思考：

1. 产生信息的过程中，本地硬件、固件、SBI、操作系统、编译器、ABI、应用程序、键鼠、屏幕等一系列软硬件设备是否可信？

2. 在信息存储的过程中，如何做到选择性可见（仅对目标对象开放）？文件的权限管理是否遵守 KISS 原则？若采用加密的方式进行存储，加密的熵值是否足够大？

3. 在信息传输的过程中，如何做到可靠传输，防止信息被窃取、篡改、伪造？

4. 如何防范社会工程？世界头号黑客 Kevin Mitnick 曾说过：“人是最薄弱的环节。你可能拥有最好的技术、防火墙、入侵检测系统、生物鉴别设备，可只要有人给毫无戒心的员工打个电话……”。Kevin 的著作 The Art of Deception淋漓尽致地展现了社会工程的效果。

围绕信息的生命周期是系统安全的一个实例，也可以围绕安全实现的四大手段“完整性、访问控制、随机化、隔离”来琢磨安全问题，这里暂不展开。当然，系统安全的思想不可能解决一切安全问题，在运用时必须反思其存在的前提是什么。毕竟盲目地运用任何一种理论，而不加考虑其前提，毫无疑问是一种愚蠢。那么系统安全的前提是什么？

笔者认为运用系统安全思维分析问题的前提是：不信任计算的参与方。这里的参与方不仅指人，也泛指计算用到的一切设备（如交换机、路由器、DNS 服务器、IP 协议）。假如你信任计算的参与方，那么就不需要考虑安全。比如 1973年 Vint Cerf 和 Bob Kahn 发表 A protocol for Packet Network Interconnection建立 Internet 后，在 1974年 ARPANET 的实践中，参与计算的节点总共只有 UCLA, SRI, UCSB, UTAH 四个，即便你骗骗我或者我骗骗你，也捞不到好处，那自然就没有必要考虑安全问题。

以上是笔者近一段时间学习安全的感悟，仅供读者参考，欢迎交流、批评与指正。最后有一句话希望与各位共勉：

在安全面前，我永远是个孩子。