差分隐私（Differential Privacy，DP）是密码学中的一种手段，可以提高从统计数据库进行数据查询的准确性，同时帮助最大限度减少识别其具体记录的机会。DP 一般分为：CDP（Centralized Differential Privacy）、LDP（Local Differential Privacy）。

一、CDP

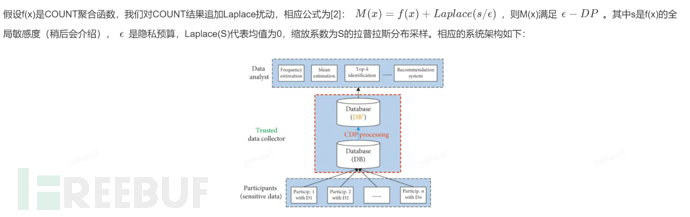
1.1 基本定义

保护效果：查询者无法判断特定样本是否在一个数据集当中。

1.2 应用举例

1.3 全局敏感度

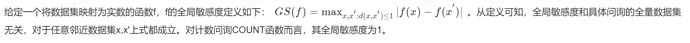
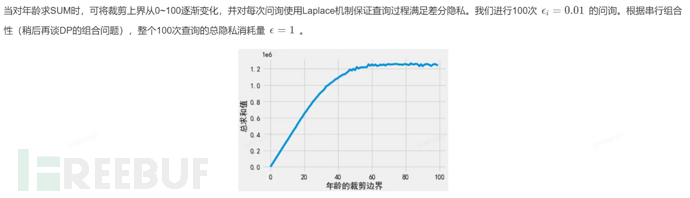
1.4 数据裁剪

COUNT 函数的 GS 始终为 1，但是 SUM 函数的 GS 就不好说了，因为这要看 SUM 作用于哪个属性列，如：年龄和收入应用 SUM 就有很大差异。如 1.2 所述，我们应用 Laplace 扰动机制时需要 f (x)（此处为 SUM）的有界全局敏感度，但 SUM 显然不容易做到，因此需要对待处理的列进行裁剪处理，以得到 f (x) 的有界全局敏感度。有两点需要特别注意：

• 在裁剪造成的信息损失与满足差分隐私所需要的噪声间进行 trade off，一般裁剪后要尽可能保留 100% 的信息。

• 不能通过查看数据集来确定裁剪边界，这可能会泄露信息，同时也不满足差分隐私的定义。

那我们应该如何对属性列进行裁剪动作，一般有如下两个做法：

• 根据数据集先天满足的一些性质来确定裁剪办界。如人的年龄一般在 0~125 岁之间。

• 采用差分隐私问询估计选择的边界是否合理。先通过数据变换把属性列映射为非负值，然后将裁剪下界置 0，逐渐增加上界，直至问询输出不变。

1.5 向量值函数及其敏感度

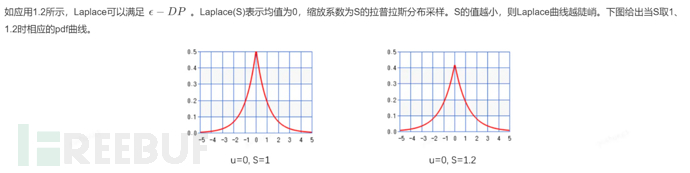
1.6 Laplace 机制

1.7 Gaussian 机制

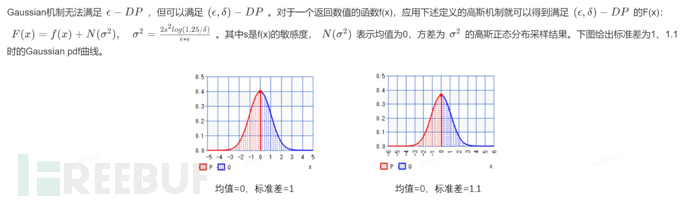
1.8 Laplace vs Gaussian

向量值 Laplace 机制需要使用 L1 敏感度，而向量值 Gaussian 机制 L1 和 L2 敏感度都可以使用。在 L2 敏感度远低于 L1 敏感度的场景下，Gaussian 机制添加的噪声要小得多。向量值 Laplace 和 Gaussian 的发布规则为：

1.9 指数机制

前述 Laplace 和 Gaussian 机制的回复都是数值型的，只需要直接在回复的数值结果上添加噪声即可。如果我们想从一个备选回复集合中选出最佳结果，同时又保证回复过程满足差分隐私，那应该怎么办呢？一种可行的方法是使用指数机制。首先，定义一个备选回复集合；然后，再定义评分函数，评分函数输出备选集合中每个回复的分数；分数最高的回复就是最大回复。指数机制通过返回分数近似最大的回复来实现差分隐私保护。

可以看到，与Laplace机制相比，指数机制的不同之处在于总会输出集合R中的一个元素。

如下我们给出有限集合的指数机制代码样例

options =adult['Marital Status'].unique()defscore(data,option):returndata.value_counts()[option]/1000defexponential(x,R,u,sensitivity,epsilon):scores =[u(x,r)forr inR]# 计 算R中 每 个 回 复 的 分 数 probabilities =[np.exp(epsilon *score /(2*sensitivity))forscore inscores]# 根 据 分 数 计 算 每 个 回 复 的 输 出 概 率  probabilities =probabilities /np.linalg.norm(probabilities,ord=1)# 对 概 率 进 行 归 一 化 处 理 ， 使 概 率 和 等 于1returnnp.random.choice(R,1,p=probabilities)[0]# 根 据 概 率 分 布 选 择 回 复 结 果exponential(adult['Marital Status'],options,score,1,1)# 输出 'Married-civ-spouse'r =[exponential(adult['Marital Status'],options,score,1,1)fori inrange(200)]pd.Series(r).value_counts()# output: Married-civ-spouse 185     Never-married 15

报告噪声最大值

当R为有限集合时，指数机制基本思想是从集合中选择元素的过程满足差分隐私。可以用拉普拉斯机制对此思想进行朴素实现：

def report_noisy_max(x, R, u, sensitivity, epsilon):
    scores = [u(x, r) for r in R]     # 计算R中每个回复的分数
    noisy_scores = [laplace_mech(score, sensitivity, epsilon) for score in scores]    # 为每个分数增加噪声
    max_idx = np.argmax(noisy_scores)   # 找到最大分数对应的回复索引号
    return R[max_idx]   # 返回此索引号对应的回复
report_noisy_max(adult['Marital Status'], options, score, 1, 1)   # 输出'Married-civ-spouse'

r = [report_noisy_max(adult['Marital Status'], options, score, 1, 1) for i in range(200)]
pd.Series(r).value_counts()  #output: Married-civ-spouse 196    Never-married 4

1.10 组合性与后处理性

在相同的输入数据上发布多次差分隐私机制保护下的结果时，串行组合性给出了总隐私消耗量。具体内容为：

二、LDP

2.1 LDP 基本定义

保护效果：其他角色（客户端或中心服务器）无法区分客户端A中的不同样本。相应的算法架构如下：

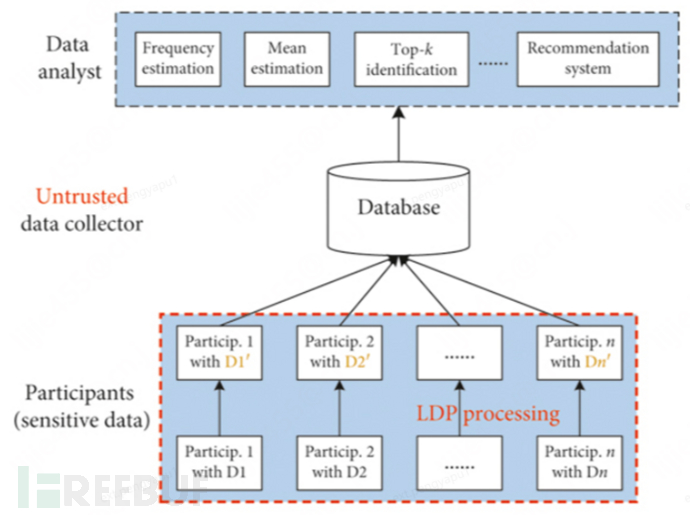
2.2 LDP 经典算法

基于随机响应

•二值离散变量：W-RR，举例见2.3

•多值离散变量（二进制编码）：RAPPOR、SHist

•多值离散变量（改进概率分布）：K-RR、GRR、ORR

•处理多维数值变量：pMeanEst、Harmony-mean(采样)

基于信息论的干扰机制

•Compression

•Distortion

2.3 LDP 举例 - 随机应答

有 n 个用户，假设 X 病患者的真实比例为 Π，我们希望对这个比例进行统计。于是我们发起一个敏感问题：“你是否为 X 病患者？”，每个用户的答案是 yes or no。出于隐私性考虑，用户可能不会给出正确答案 [5]。

我们可以对每位用户的回答加一些数据扰动。比如：用户正确回答的概率为 p，错误回答概率为 (1-p)。这样就不会准确知道每位用户的真实答案，相当于保护了用户隐私。按此规则我们统计回答 yes 与 no 的用户占比。

DP 在机器学习领域的应用、基于 Gaussian 机制实现 LDP 的原理请听下回分享。

实例验证

共有n=50人（已知），其中10人为阳（未知），40人为阴（未知）。每人以p=0.8概率真实上报（已知）。则统计结果如下：

•阳性统计值n1=10*0.8+40*0.2=16

•阴性统计值=40*0.8+10*0.2=34

修正的阳性值=50*(-1/3)+160/6=10

参考资料

1.Balle B, Wang Y X. Improving the gaussian mechanism for differential privacy: Analytical calibration and optimal denoising[C]//International Conference on Machine Learning. PMLR, 2018: 394-403.

2. https://programming-dp.com/

3.Cynthia Dwork, Aaron Roth, and others. The algorithmic foundations of differential privacy. Foundations and Trends® in Theoretical Computer Science, 9(3–4):211–407, 2014.

4.Xiong X, Liu S, Li D, et al. A comprehensive survey on local differential privacy[J]. Security and Communication Networks, 2020, 2020: 1-29.

5.LDP 随机响应技术举例： https://zhuanlan.zhihu.com/p/472032115

作者：京东科技 李杰

内容来源：京东云开发者社区