0x1.前言

提到这个你可能有些不屑一顾，如果pq非常相近的话直接用yafu就可以解出来，根本不需要我们去操心解，那写这篇文章的意义是什么，没错，之前的我也是这么想的，但实际上不是，事实证明，有些东西还是要明白一些原理才能属于你，不然有些题目稍稍变化你就不会了。

所以我今天就来好好记录一下这个问题。

0x2.正文

1.题目表现和yafu分解

首先pq的值相近是什么意思，在题目中，一般是指这样的意思：

from Crypto.Util.number import getPrime
import gmpy2
p = getPrime(512)
q = gmpy2.next_prime(p)
n=p*q
print('n =',n)

直接生成一个实例来演示吧：

n = 149508848441616715934297319023960757580837139746636486446093766820602595577720613880522359931376776640771560399865570788752926866918099448386204160338951577084579042581094657939545555751085950319193925075988080113525569558968885659546782419751524189916167947489803707492932640059831396220643698853028753007377

嗯，这种再常见不过了，我们一般用yafu可以直接分解出两个p和q：

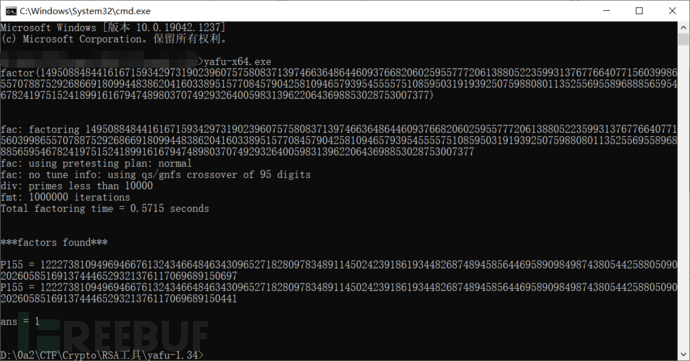
然后之后的运算就非常简单了，问题在于，如果让我们自己用脚本算怎么算？

2.Python脚本分解

仔细想想这个问题，其实方法有好几种，这里一一列举一下。

2.1.简单思路

我们将他直接取平方根，然后取整之后的值一定在两个数之间，因为他们是通过next_prime连接的，所以可以断定他们之间一定没有质数，所以我们可以再直接通过一个next_prime得到较大的那个质数p，那么另一个质数q我们也就知道了。

脚本如下：

import gmpy2
n = 149508848441616715934297319023960757580837139746636486446093766820602595577720613880522359931376776640771560399865570788752926866918099448386204160338951577084579042581094657939545555751085950319193925075988080113525569558968885659546782419751524189916167947489803707492932640059831396220643698853028753007377
tmp=gmpy2.iroot(n,2)[0]
p=gmpy2.next_prime(tmp)
q=n//p
print("p=",p)
print("q=",q)

道理很简单，运行看看：

可以发现和之前yafu计算的答案是一样的。

2.2.另一种解法

这种解法和上一种思路基本一致，也是利用求n的平方根来得到结果，那么区别在哪呢？首先，它能够一次性获得p和q两个解，另外它还有其他好处，我们先看方法：

import gmpy2

def factor(n):
a=gmpy2.iroot(n,2)[0]
while True:
a+=1
b2=a*a-n

if gmpy2.is_square(b2):
 b2=gmpy2.mpz(b2)
 b,xflag=gmpy2.iroot(b2,2)
 assert xflag
 return (a-b,a+b)

n = 149508848441616715934297319023960757580837139746636486446093766820602595577720613880522359931376776640771560399865570788752926866918099448386204160338951577084579042581094657939545555751085950319193925075988080113525569558968885659546782419751524189916167947489803707492932640059831396220643698853028753007377
p,q=factor(n)
print("p=",p)
print("q=",q)

先看看运行结果：

嗯，答案和之前一模一样，但或许此时你又有了些许疑问，这个脚本的原理是什么？又为什么这么写？又有什么好处？

这里一一讲解。

你可以看到，这个脚本和上一个脚本还是非常不同的，那么它到底用了什么原理呢？

如果你仔细观察可以看到，返回的p和q在分解函数中实际上分别是两个临时参数a-b和a+b，这个又是咋来的呢？

a首先好说，a是n的整数平方根，这很好理解，但是b的产生是什么鬼？其中还有个令人费解的式子：b2=a*a-n，而b又是b2的平方根，这又是怎么回事？

首先列出一个式子：n=p*q，这个式子的正确性毫无疑问，代换到上面提到的p=a-b,q=a+b，那么就是n=(a-b)*(a+b)，可以发现其实就是n=a*a-b*b，而b2不就是b的平方吗，所以有n=a*a-b2，这个式子如果成立的话，那么b2的产生式：b2=a*a-n也就没啥问题了。

所以我们发现，这个代码绕这么一大圈，其实就是在遍历a的前提下，求出所有可行的b，让其可以满足n=(a-b)*(a+b)这个式子，从而得到p和q。

而a的值在整个爆破过程中是从小到大的，相应的，b的值也是从小到大的，因为b*b=a*a-n，随着a的增大，b也会变大，而与之相应的，两个解：a-b和a+b，之间的差距也会变大，而在最开始爆破的时候我们可以认为b=0，此时的a*a相当于在0~n之间求解的最‘中间’，这样我们就可以明白了，这个脚本正是从n的平方根这个‘中间值’开始，逐渐向两边扫描，直到得到解或者a-b==0，所以原理上它可以爆破出所有解。

好的，原理我们明白了，我们也就知道，这个脚本其实是一个爆破脚本，它会尝试每一种可能性，直到得到解，所以这个脚本也只能在初始值和解相近的时候使用，如果从0开始爆破，那得爆破到猴年马月去。

所以为什么要这么做？

可以发现，这个脚本是爆破脚本，实际上并没有第一个脚本那样思路简单明了，那么它有什么用呢？

好处就在于，这个脚本是一个爆破脚本，所以它能爆破出所有可能的解，我们这道示例自然看不出什么，因为它只有一个解，当只有一个解时使用上面这两种脚本都能得到正确解。

同时，它也不会受到next_prime的限制，如果解不是质数它也会求出解。

这在一些稍微改变的题中是非常有用的。

下面我们用例子来说明这个解题方法。

3.题目变种

3.1.两组相近的因子时

这里引用的是最近的一场比赛绿城杯的比赛的一部分：【绿城杯】RSA2-PLUS

部分源码如下：

from Crypto.Util.number import *
import gmpy2
from flag import flag
assert flag[:5]==b'flag{'
​
m1 = bytes_to_long(flag[:20])
p  = getPrime(512)
p1 = gmpy2.next_prime(p)
q  = getPrime(512)
q1 = gmpy2.next_prime(q)
n1 = p*q*p1*q1
print('n1 =',n1)
e = 0x10001
c1 = pow(m1,e,n1)
print('c1 =',c1)
​
#n1 = 6348779979606280884589422188738902470575876294643492831465947360363568026280963989291591157710389629216109615274754718329987990551836115660879103234129921943824061416396264358110216047994331119920503431491509529604742468032906950984256964560405062345280120526771439940278606226153077959057882262745273394986607004406770035459301695806378598890589432538916219821477777021460189140081521779103226953544426441823244765828342973086422949017937701261348963541035128661464068769033772390320426795044617751909787914185985911277628404632533530390761257251552073493697518547350246993679844132297414094727147161169548160586911
#c1 = 6201882078995455673376327652982610102807874783073703018551044780440620679217833227711395689114659144506630609087600915116940111002026241056808189658969089532597757995423694966667948250438579639890580690392400661711864264184444018345499567505424672090632235109624193289954785503512742400960515331371813467034511130432319427185134018830006918682733848618201088649690422818940385123599468595766345668931882249779415788129316594083269412221804774856038796248038700275509397599351533280014908894068141056694660319816046357462684688942519849441237878018480036145051967731081582598773076490918572392784684372694103015244826

这里看起来和上面的题目类似，不同的是n由4个质数因子组成，其中两个成对近似相等，这时候当然也不能用第一个脚本那种思路了，因为不管几次根都不太可能next_prime正好等于真正的p和q，这时候我们也可以直接用yafu分解试试：

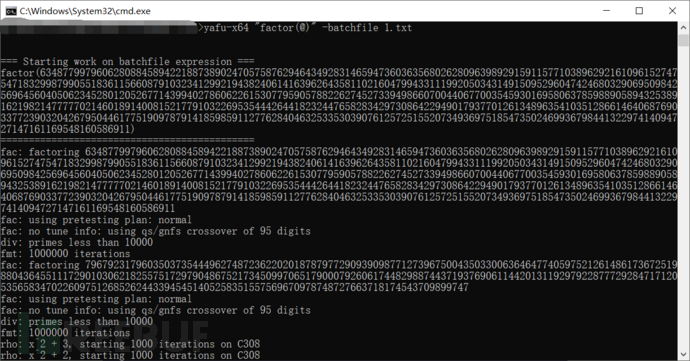
一直运算就会没完没了，终止运算可以发现分解出了一个解，但是这个解其实并不是质数：

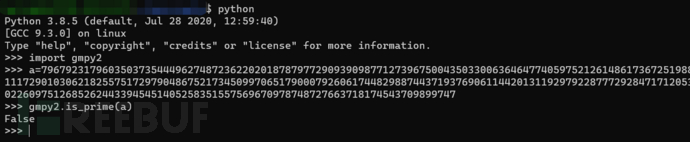
所以我们算出的这个解并不是n的4个因子其中一个，而是其中两个的乘积，而用n除以这个解得到的值则是另外两个因子的乘积，这对我们求出欧拉函数phi并没有什么用处。

那么我们怎么才能得到完整的4个因子的值呢？

先看一下这4个因子的构造吧：

p  = getPrime(512)
p1 = gmpy2.next_prime(p)
q  = getPrime(512)
q1 = gmpy2.next_prime(q)

也就是说，p和p1相近，q和q1相近，我们并不知道yafu此时求出的是谁和谁的乘积，也许是p*q或者p1*q1，也许是p*q1或者q*p1，不管怎么样，我们发现一个十分有趣的特点，那就是在n1的平方根这个‘中间值’两侧有这两组非常相近的解：(p*q)*(p1*q1)，(p*q1)*(q*p1)，那么我们如果使用上面的第二个脚本那种方法，我们就可以在短时间内爆破出这两组非质数的解，因为我们知道它其实是从‘中间’开始往两边爆破的，一旦我们两组解都有了，求它们的公因数就能得到q或p的值，从而得到所有4个因子的值。

这里需要注意的是n的分解并不是只有这2组解，而是有共8组解，包括(p)*(p1*q*q1)，(p*p1)*(q*q1)这样的解，只不过我们知道那两组解十分接近我们爆破的起始地点，这就造成了我们的利用。

有了这个思路我们就可以写出以下代码：

import gmpy2

def fermat_factorization(n):
factor_list = []
a = gmpy2.iroot(n,2)[0]
while True:
a += 1
b2 = a * a - n

if gmpy2.is_square(b2):
 b2 = gmpy2.mpz(b2)
 b,xflag = gmpy2.iroot(b2,2)
 assert xflag
 factor_list.append([a + b, a - b])
 if len(factor_list) == 2:
  break
return factor_list

n1 = 6348779979606280884589422188738902470575876294643492831465947360363568026280963989291591157710389629216109615274754718329987990551836115660879103234129921943824061416396264358110216047994331119920503431491509529604742468032906950984256964560405062345280120526771439940278606226153077959057882262745273394986607004406770035459301695806378598890589432538916219821477777021460189140081521779103226953544426441823244765828342973086422949017937701261348963541035128661464068769033772390320426795044617751909787914185985911277628404632533530390761257251552073493697518547350246993679844132297414094727147161169548160586911
factor_list = fermat_factorization(n1)
X1,Y1=factor_list[0]
X2,Y2=factor_list[1]
assert X1*Y1==n1
assert X2*Y2==n1
p=gmpy2.gcd(X1,X2)
q=X1//p
p1=gmpy2.gcd(Y1,Y2)
q1=Y1//p1
print('p=',p)
print('q=',q)
print('p1=',p1)
print('q1=',q1)

运行，成功得到四个质数：

也许其中的数值顺序和原来可能不太一样，不过没关系，我们只要取得结果就可以了。

接下来就是正常的rsa解密步骤，这里不再累述。