数字签名是公钥密码体制下解决身份认证与内容认证问题的重要密码学技术手段。为了在传统数字签名的基础上实现身份匿名或内容隐藏等隐私保护需求，群签名、环签名、盲签名等支持隐私保护的特殊数字签名算法得到了深入的研究和广泛的应用探索。

本文对群签名、环签名、盲签名这三类特殊数字签名算法的应用需求、技术特性等内容进行研究，并介绍了各类算法在匿名支付、匿名竞标、匿名投票等场景中的不同应用方向。

一、数字签名的特殊功能需求

数字签名是一类可实现身份和内容认证的密码技术，主要用于表明签名主体对特定数据内容有效性的认可，同时能够保证签名主体身份的可验证性、数据内容的完整性（不可篡改）、签名本身的不可伪造性、签名行为的不可抵赖性等。目前，常见的传统数字签名算法包括RSA签名、ElGamal签名、Schnorr签名、DSA/ECDSA、国密SM2签名等。

传统数字签名技术实现了基本的认证功能。然而，在一些新兴应用场景中，存在身份匿名、内容隐藏等特殊的隐私保护功能需求，需要通过群签名、环签名、盲签名等特殊的数字签名技术实现。

（1）有监管身份匿名

在匿名举证、匿名竞标等场景中，用户在发布举证信息或投递标书时，为了自证身份可信与资质可靠，希望向外界证明其在特定的用户群组内，但又不希望暴露具体身份，因此需要使用支持身份匿名的数字签名技术对相关信息进行签名。同时，有必要引入一个监管角色在必要时对签名进行追溯，反推出生成签名的具体用户。群签名是解决有监管身份匿名问题的一类可行方案。

（2）无监管身份匿名

在区块链等弱中心化或多中心化场景中，为了实现完全化的匿名，用户希望只需自证其在一定的合法用户范围内，而不希望存在监管角色能够反推出签名者的身份。因此，在群签名的基础上，产生了无需群管理者角色的环签名应用需求。

（3）内容隐藏

在电子投票等场景中，认证机构需要验证投票者的投票资格并签名以提供选票的有效性，但用户又不希望认证机构获知投票的具体内容，因此，存在对内容进行盲化后再进行签名的需求，即盲签名。

群签名和环签名主要用于将签名者的身份隐藏于一整个群体之中，两者的区别在于：群签名存在监管方，支持对签名进行追踪，但在群成员撤销方面的支持度不够灵活；而环签名不存在监管方，可实现不可追踪的完全匿名性，且环签名可任意选定用户群体作为签名主体，在成员动态变化方面较为灵活。盲签名主要用于实现将待签名数据内容对签名者隐藏，使签名请求者在不泄露数据内容的情况下得到签名者的合法签名，并可满足签名的不可追踪性。

二、群签名及其应用

1、基本概念

1991年，Chaum和Heyst首次提出了群签名（Group Signature）的概念，并给出了四种群签名的初步实现方案^[1]。目前，主流的群签名算法包括CS97^[2]、BBS04^[3]等方案。

在一般的群签名方案中，群管理者负责群组的创建和群成员的加入。某个群成员可代表所在群组生成一个群签名，验证者可验证该签名由该群组中的成员签署，但无法判定具体是哪一个成员，在实现身份认证的同时保证了一定的匿名性。群管理者在必要的时候可以打开签名，追踪生成该签名的具体成员。因此，群签名是一类有监管的有条件匿名数字签名。

根据ISO/IEC 20008和GB/T 38647匿名数字签名标准的定义，群签名算法主要包括创建群、加入群、签名、验证签名、打开签名、撤销群成员等步骤，如图1所示。

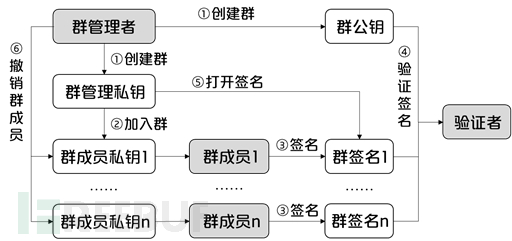
图1：群签名流程

① 创建群：群管理者生成群管理私钥（用于生成群成员私钥以及打开群签名）和群公钥（用于验证群签名）。

② 加入群：群管理者使用群管理私钥生成并分发群成员的私钥。

③ 签名：群成员使用自己的私钥对特定数据进行签名。

④ 验证签名：任意验证者可使用群公钥对群签名进行验证。

⑤ 打开签名：当存在签名者追踪等必要情况的时，群管理者可使用群管理私钥获知群签名对应的群成员身份。

⑥ 撤销群成员：与基于PKI的证书撤销机制中CA需要维护一个证书撤销列表（Certificate Revocation List, CRL）类似，群签名中的群管理者可通过公布已撤销私钥列表等手段撤销群成员的权限，使其无法生成合法的群签名。

除不可伪造性等数字签名的通用安全要求以及上述的匿名性和可追踪性外，群签名通常还需满足不可关联性和抗联合攻击等特殊安全要求。

① 不可关联性：在群管理者未打开签名的情况下，任何人无法判断两个不同的签名是否为同一个群成员所生成。

② 抗联合攻击：即使多个群成员合谋，也无法生成不可被追踪的合法群签名。

2、应用场景

群签名是一类仅支持有限匿名性的签名方案，适用于具有监管角色且存在事后身份追踪需求的场景。以下以匿名投票和匿名竞标为例分析群签名的应用场景及其局限性。

（1）匿名投票

群签名可实现有限匿名的电子投票，即能够在投票后追踪特定选票的投票者身份，具体过程如下：

① 派票：投票组织者或可信第三方作为群管理者生成群管理私钥和群公钥，并生成和分发所有投票者的群成员私钥。

② 投票：投票者使用自己的群成员私钥对投票内容进行群签名。

③ 计票：计票者可对群签名进行验证，确认投票者为合法投票者，但无法确认投票者具体身份。

④ 追踪：计票者发现存在问题的选票或投票者希望自证为某个选票的签名者时，可向投票组织者或可信第三方申请签名追踪，投票组织者或可信第三方可使用群管理私钥得到签名者的身份。

由于群管理者的存在，基于群签名的匿名投票方案支持投票者追踪，但无法实现完全无记名的投票，可考虑采用环签名作为替换实现完全匿名化的电子投票方案。

（2）匿名竞标

为了尽可能避免招标过程中存在的招标方与投标方、投标方与投标方之间的串通行为，保证招标过程的公平性，投标方可能存在匿名投标的需求，即招标方和其他投标方在结果确定前无法获知具体的投标方身份，但招标方又希望在投标前能够对投标方的身份进行资格认证。该类匿名竞标的需求可考虑采用群签名作为解决方案，具体方法如下：

① 创建群：可信第三方可作为群管理者，生成群管理私钥和群公钥。

② 加入群：可信第三方作为密钥分发者，将所有拟参加竞标的合格投标方加入群组并分别分发群成员私钥。

③ 群签名：投标方可对标书进行群签名后，通过匿名信道发送给招标方实现匿名投标。

④ 验证签名：招标方可验证投标者为事先确定的合法投标方之一，但无法确定投标者的具体身份。

此外，在基于区块链的公开竞标场景中，所投标书等信息在链上公开，基于群签名的匿名竞标还可防止投标方获知其他标书对应竞标方的身份。

在上述解决方案中，存在可信第三方的安全假设。如果招标方本身作为可信第三方或与可信第三方存在共谋，可通过群签名的签名打开机制追踪到生成签名的具体投标方，无法满足真正的匿名性需求。因此，可考虑采用不存在群管理者角色的不可追踪匿名签名方案（如环签名）解决不存在真正可信第三方情况下的匿名竞标问题。

三、环签名及其应用

1、基本概念

2001年，Rivest、Shamir和Tauman提出了无需群管理者的匿名签名方案^[4]。由于其签名生成结构为环状，因此将该类签名方案命名为环签名（Ring Signature）。在此之后，许多具有相似特性的无监管匿名签名方案都以环签名命名。目前，主流的环签名算法包括RST01^[4]、FS07^[5]、LSAG^[6]等方案。

与群签名中群管理者可追溯具体签名者不同，环签名不存在管理者角色，具有不可追踪性，签名者可任意选定一定数量的用户作为环成员实现匿名签名，其最初用于实现完全匿名地泄露秘密信息。

根据ISO/IEC 20008和GB/T 38647匿名数字签名标准的定义，环签名算法的一般流程如图2所示。

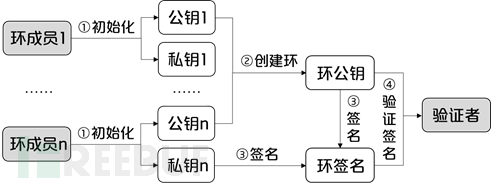
图2：环签名流程

① 初始化：每个用户拥有自己的公钥和私钥。

② 创建环：签名者选择若干个用户公钥作为环成员公钥以创建环，并生成环公钥。

③ 签名：签名者使用环公钥和自己的私钥生成环签名。

④ 验证签名：验证者可使用环公钥对环签名进行验证。

由于环签名机制需要签名者自行选择若干其他用户的公钥作为混淆进行环签名，因此在选取公钥列表创建环的过程中需要进行如下因素的考量：

① 性能：在主流的环签名算法方案中，签名生成效率和签名大小通常与环成员数量成正比，因此需要合理控制环成员数量上限以保证环签名性能。

② 隐私性：在创建环时，环成员公钥的数量越多，则在众多环成员中发现真正签名者的可能性越小，因此对于签名者身份的隐私保护效果越好。

综上所述，在应用环签名方案时应综合考虑性能和隐私性因素，通过理论分析和实际测试选择最为合适的环成员数量。

2、应用场景

作为不支持监管或仅支持弱监管的完全匿名化自组织签名方案，环签名天然适用于弱中心化的应用场景，例如区块链等。以下以匿名投票和匿名虚拟货币场景为例说明环签名的应用。

（1）匿名投票

环签名可实现无需注册过程的匿名投票，即不需要在投票前向认证机构进行身份认证。方案的简化过程如下：

① 投票：投票者使用包含所有合法投票者的公钥列表以及自己的私钥，对投票内容进行环签名。

② 开票：计票者可对环签名进行验证，确认投票者为合法投票者，但无法确认投票者具体身份。同时，可通过LSAG等环签名方案的可关联性防止同一投票者重复投票的问题。

与基于群签名的匿名投票方案相比，基于环签名的方案不存在群管理者角色，无需生成和分发群成员私钥的初始过程，且任何人无法对签名者身份进行追踪，实现了更为彻底的完全匿名投票。

但是，在存在众多合法投票者的情况下，使用完整的公钥列表进行环签名不具有现实可行性，因此仍需采用其他技术手段（如盲签名）实现隐藏身份或内容的匿名投票。

（2）匿名竞标

为了在基于群签名的匿名竞标方案基础上实现更充分的匿名性，可考虑将群签名替换为环签名进行方案设计，具体过程如下：

① 环签名：投标方使用自己的私钥以及所有拟参与竞标的投标方公钥创建环，并对标书进行环签名，然后通过匿名信道发送给招标方实现匿名投标。

② 验证：招标方可验证投标者为拟参与竞标的投标方之一，但无法确定投标者的具体身份。

由于环签名不存在群管理者打开签名的机制，无法对中标结果进行直接的身份揭示，在一定程度上也影响了方案的完备性。同时，由于符合资质的投标方名单可在投标前由招标方确定，并无在环签名中由竞标方自行选取的必要性。因此，对于参与方（投标者）范围确定且存在中间组织方（招标方）的招标场景，更加适合采用基于群签名的匿名竞标方案。

（3）匿名虚拟货币

在比特币等不支持隐私保护的虚拟货币中，虽然无法通过区块链获知交易相关方的具体身份，但每一笔交易的发起方和接收方地址是公开的，依然可通过对地址的关联交易进行分析获知所有的交易流动情况。为了实现更好的隐私保护性，同时又不影响虚拟货币的交易功能，可引入环签名等隐私保护技术。

CryptoNote是一种用于实现虚拟货币隐私性的应用层协议，门罗币的底层实现即基于CryptoNote协议。门罗币通过CryptoNote协议实现了交易发起方的不可追踪性、交易接收方的不可关联性、交易金额的隐匿性等隐私特性。其中，交易发起方的不可追踪性基于环签名技术实现。在CryptoNote 2.0白皮书中，主要基于FS07方案实现了一次性环签名功能，用于实现虚拟货币交易过程中用户身份的匿名性。目前，基于CryptoNote协议的门罗币已改用LSAG方案作为环签名实现方式。

在CryptoNote中，每次交易都会由交易发起方生成独立的一次性环签名，将自己的公钥混淆在若干个其他无关用户中（目前门罗币要求每次交易的环成员数量为11个），区块链网络无法获知交易发起方的具体地址，因此无法进一步分析关联交易情况。CryptoNote中的环签名的交易机制如图3所示。

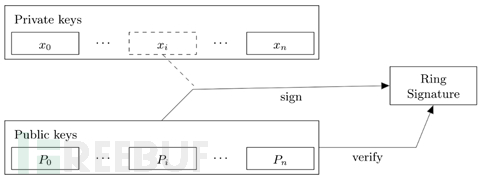
图3：CryptoNote中的环签名

用户在发起交易时，使用自己的一次性私钥并随机选取包含对应公钥的公钥列表对交易信息进行环签名，区块链验证者可通过该公钥列表对环签名进行验证，判定交易发起用户在该公钥列表内，但无法将交易与其中的具体公钥地址进行关联。

为了避免由于矿工无法获知交易双方的真实地址而可能导致无法判断“双花”（Double Spending）的问题，CryptoNote协议需要交易发起方使用公私钥对为每一笔交易生成一个唯一的密钥镜像，矿工可根据密钥镜像判断是否发生“双花”。

四、盲签名及其应用

1、基本概念

1982年，Chaum首次提出了盲签名（Blind Signature）的概念^[7]，最初用于实现不可追踪的电子支付。目前，主流的盲签名算法包括盲RSA签名、盲Schnorr签名、Okamoto93^[8]等方案。

直观而言，盲签名即签名请求者可委托签名者在不泄露文件内容的情况下实现代理签名。以保密信封为例，签名请求者将待签名的隐私文件盖上复写纸放入信封内密封后交给签名者，签名者可直接在信封上签名并交还给签名请求者，由于复写纸的存在，签名请求者将文件从信封中取出后即得到了签名者对该文件的签名，实现了签名者在不知道文件内容的情况下对文件进行签名。

在盲签名的算法实现中，将文件放入信封的过程即为使用随机的盲化因子对原始数据进行盲化的过程，从信封中取出文件的过程即为使用对应的盲化因子对盲签名进行解盲的过程。此外，与保密信封的例子不同，盲签名算法中签名请求者无法对解盲后的签名对应的数据进行篡改。

与传统的数字签名相比，盲签名一般具有盲化性和不可追踪性两个特性：

① 盲化性：签名者无法通过盲化后的数据反推出原始数据。

② 不可追踪性：签名者无法将签名请求者解盲后的签名与其之前签署的盲签名进行关联，即无法关联原始数据和签名行为。

盲签名算法的一般流程包括盲化、盲签名、解盲、验证签名等步骤，如图4所示。

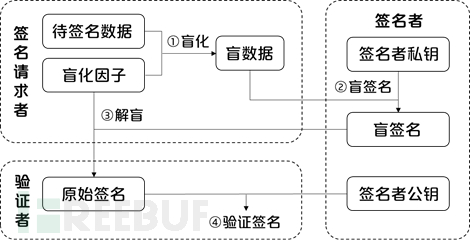
图4：盲签名流程

① 盲化：签名请求者生成随机数作为盲化因子，并对待签名数据进行盲化处理，并将盲化后的数据发送给签名者。

② 盲签名：签名者使用自己的私钥对盲化后的数据进行签名，并将盲签名发送给签名请求者。

③ 解盲：签名请求者使用盲化因子对盲签名进行解盲处理，得到原始数据的签名。

④ 验证签名：解盲后的签名即为签名者的合法签名，验证者可直接使用签名者的公钥进行验证。

在盲签名场景中，由于盲化性和不可追踪性的存在，签名者无法对签名的使用进行跟踪和追责，可能存在签名请求者滥用签名的行为。为此，可通过在盲签名方案中引入可信第三方构造公平盲签名方案，以实现一定的可追踪性。公平盲签名的一般流程如下：

① 签名请求者首先需要将待签名数据和盲化后的数据发送给可信第三方进行存证，可信第三方向签名请求者提供认证信息。

② 签名请求者将待签名的盲化数据和认证信息发送给签名者请求签名。

③ 签名者首先验证签名请求者的认证信息，确认其已向可信第三方登记后对盲化数据进行签名，并保留盲化数据作为证据。

④ 当后续存在追责需求时，签名者可将保留的盲化数据发送给可信第三方请求取证，可信第三方可通过盲化数据查询到原始数据和签名请求者身份。

2、应用场景

（1）匿名投票

与基于环签名的匿名投票机制不同，在具有认证机构的匿名电子投票场景中，认证机构需要对每一张投出的选票进行认证，防止不具备投票资格的人进行投票或合法投票者多次刷票，但同时为了保证投票的无记名性，投票者又不希望投票内容被认证机构获知。因此，可通过盲签名技术实现上述应用需求：

① 认证：投票者使用盲化因子对投票内容进行盲化，并将盲化后的选票发送给认证机构，进行投票资格认证。

② 签名：认证机构可通过任意方式对投票者的身份进行认证，确认其具有投票资格且非重复投票行为后，将其身份信息记录在已投票列表中，并使用认证机构的私钥对盲化后的选票进行签名，并将其返回给投票者。

③ 投票：投票者使用盲化因子对盲签名进行解盲处理，得到选票的原始签名后，将选票及其签名通过匿名信道发送给计票方。

④ 计票：计票方使用认证机构的公钥对选票签名进行验证，确认该投票合法后，根据选票内容进行计票。

根据盲签名算法的盲化性和不可追踪性，认证机构无法在签名时获知选票内容，也无法在事后将其签名过的选票与投票人进行对应，实现具有认证机构情况下的匿名投票。此外，由于数字签名本身的不可篡改性质，投票者也无法在认证机构进行盲签名后篡改选票内容。

（2）匿名支付

为了实现与传统货币相同的匿名性、可流通性、防伪性、不可复制性等特性，可基于盲签名设计匿名支付方案。假设只存在同一银行内的匿名交易，匿名支付方案的兑换和支付简化步骤如下：

① 兑换：用户随机生成匿名支付序列号（每个序列号具有相同的固定面额），使用随机盲化因子对该序列号进行盲化处理，并发送给银行进行盲签名，银行在不知道序列号的情况下对序列号进行签名并返回给用户，同时将相应金额从用户的银行账户转到匿名支付账户，即完成了匿名支付金额的兑换。

② 支付：用户对盲签名进行解盲处理，得到包含银行签名的匿名支付序列号。用户可将该序列号及其签名发送给收款方（可流通性），收款方首先使用银行的公钥对签名进行验证（防伪性），然后将序列号发送给银行进行兑现。为了防止重复使用（不可复制性），银行首先查询该序列号是否已被使用，如果尚未使用，则将其存入已使用序列号列表中，并将相应款项从用户的匿名支付账户转到收款方的账户中。

由于盲签名的不可追踪性，银行无法将发行出的盲化序列号和支付收到的序列号进行关联对应，即无法获知支付过程中付款方的用户身份，满足货币的匿名性要求。同时，为了在货币匿名性的基础上实现一定的监管要求，可考虑采用包含可信第三方的公平盲签名方案。

五、总结

作为三类支持隐私保护的数字签名技术，以BBS04方案为代表的群签名、以LSAG方案为代表的环签名、以盲RSA签名为代表的盲签名在传统数字签名的基础上分别解决了可监管身份匿名、自组织身份匿名、数据内容隐藏等不同场景问题，在电子支付与电子商务等具有一定匿名性和隐私性需求的领域有着广泛的应用价值。

参考文献

[1] Chaum D, Van Heyst E. Group signatures[C]//Workshop on the Theory and Application of of Cryptographic Techniques. Springer, Berlin, Heidelberg, 1991: 257-265.

[2] Camenisch J, Stadler M. Efficient group signature schemes for large groups[C]//Annual International Cryptology Conference. Springer, Berlin, Heidelberg, 1997: 410-424.

[3] Boneh D, Boyen X, Shacham H. Short group signatures[C]//Annual International Cryptology Conference. Springer, Berlin, Heidelberg, 2004: 41-55.

[4] Rivest R L, Shamir A, Tauman Y. How to leak a secret[C]//International Conference on the Theory and Application of Cryptology and Information Security. Springer, Berlin, Heidelberg, 2001: 552-565.

[5] Fujisaki E, Suzuki K. Traceable ring signature[C]//International Workshop on Public Key Cryptography. Springer, Berlin, Heidelberg, 2007: 181-200.

[6] Liu J K, Wei V K, Wong D S. Linkable spontaneous anonymous group signature for ad hoc groups[C]//Australasian Conference on Information Security and Privacy. Springer, Berlin, Heidelberg, 2004: 325-335.

[7] Chaum D. Blind signatures for untraceable payments[C]//Advances in cryptology. Springer, Boston, MA, 1983: 199-203.

[8] Okamoto T. Provably secure and practical identification schemes and corresponding signature schemes[C]//Annual international cryptology conference. Springer, Berlin, Heidelberg, 1992: 31-53.