摘要

文本信息总是在新建，传播，每天每个人至少会发出十条信息，由于频繁使用致使它们并未被加密。因此人们并不能通过短信交换机密信息。本文中，我们开发出了一款新的加密算法，它利用了帕斯卡三角和谢尔宾斯基三角相关的概念。要论述的做法是利用帕斯卡三角做替换和利用谢尔宾斯基三角做置换。这个方法在现实生活中简单、易行。而且攻击者很难从密文中破译。但此方法在暴力破解和词频攻击中依然很脆弱。

关键词

加密，替换，置换，帕斯卡三角，谢尔宾斯基三角

一、简介

由于其实用性及科技的普及，通讯用户之间传递短消息的方法在社交媒体、聊天应用、电子邮件等领域越来越广泛。在这些领域中传播的信息难免有些是机密并且对用户很敏感的。因此，非常有必要加密这些消息。加密等机制就可以提供机密服务。替换法和置换法就经常用来加解密文本信息[15]。本文中，我们将使用一种基于替换法和置换法的用于加解密的算法，这种算法基于要论述的帕斯卡三角和谢尔宾斯基三角的概念。帕斯卡三角的概念用于在一种特殊的模式下对纯文本中字符进行异或运算，运算结束后得到我们想要的密文。

二、参考文献

这一节里，我们会提到一些经典和现代加密数据技术的概述。加密文本使用了前辈们介绍过的一些不同的简单方法 [5, 7-9, 12, 13]

2.1 古典加密

凯撒密码是已知的最简单的加密方式之一。此方法由Julius Caesar命名，他使用这种方法与他的部下们通讯。这是一种利用按照字母表的顺序将纯文本内容移动一定字母实现加密的算法。然而这种算法并不能保证通讯的安全性并且很容易就可能被人们手动破解出来。该方法应用了下列等式(1)(2)[15]来实现加解密：

加密：C = (P+K) mod 26解密：P = (C-K) mod 26

PlayFair加密是一种多字符加密，每次加密两个字符。它使用一个5×5的矩阵来进行加解密。该方法加密的是字母对而不是单纯地将单个字母进行替换操作。PlayFair算法很难破译，因为用来对付简单替换字母加密的频率分析方法对它无效。频率分析虽然有可能破译出密文，但是要经过25×25=625钟字母组合而不是25钟可能出现的文本[15]Vigenere加密是一种多字符替换加密算法。也就是说该加密算法可以将一段纯文本中的单字母替换为多字母密文。这种替换取决于字母在文中的位置。

Vigenere加密使用的是26×26的Vigenere字母表[15]栅栏加密技术是将明文按照对角线序列书写并将行序列组合成密文的加密方法。在栅栏密码中，我们将原文中的空格删除并将字母写到Z字形图案中。破解栅栏密码的关键就是栅栏数。[15]Hill密码中，利用矩阵乘法的知识进行加密。它根据密钥的大小将明文分解成子文本，并把每一个子文本与密钥矩阵相乘得到密文文本矩阵。[15]加解密的等式如下(3)(4)：加密：C=PK mod 26解密：P=CK^-1 mod 26PS：这里的C代表明文，P代表密文，K代表密钥矩阵

2.2 文本信息加密方法

Acharya等[1]提出了一种利用矩阵变换的图像加密方法。Cooper等[2]提出了一种利用帕斯卡三角的公钥加密系统。Dinesh P. Baviskar等[3]开发了一种基于Android(安卓)系统的利用矩阵的信息加解密算法。加密算法在保护机密信息免遭黑手方面起着至关重要的作用。运行算法需要消耗大量的计算机资源，如CPU寿命、内存和加密时间[6]。矩阵重排序的概念用于加密数字图像的例子也可以在本文中见到[10]。在[11]中，作者利用从SHA-512和MD5散列函数的随机参数派生的密钥开发了一种新的对称密码系统。在[14]中，利用了帕斯卡三角的新加密技术来加解密数字图像

三、要论述的加密方法

接下来要进行论述的方法引用帕斯卡三角概念进行替换和引用谢尔宾斯基三角概念进行置换从而加密数据。起初，明文字符以三角形排列。然后我们利用帕斯卡三角把每一个字母进行按位异或操作得到新的密文字母。谢尔宾斯基三角加密则是利用谢尔宾斯基三角来去的加密消息的。

3.1 帕斯卡三角

帕斯卡三角是由二项式系数构成的三角形数组。每行中的条目从左边开始编号为k = 0，并且通常相对于邻行中的数字交错排列。行和列这两个参数使得我们可以在帕斯卡三角形的第n行第k列找到相应的二项式系数(nk)，这种结构来源于如[4]中所说的帕斯卡三角原则中的二项式系数。那么就有如下两个等式(5)(6)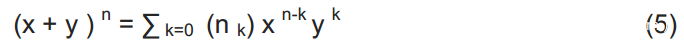：其中一个帕斯卡三角示例如图1所示：

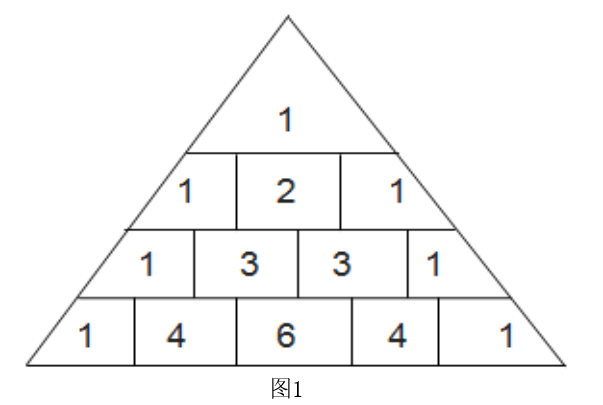
3.2 谢尔宾斯基三角

谢尔宾斯基三角是由一个等边三角形按照如下方法连续去除一些三角形构成的：

a.从一个等边三角形开始 

b.将其均分为四个全等的等边三角形并去除中心的三角形 

c.对每个小三角形重复b的步骤

谢尔宾斯基三角的形成过程示例如图2所示：基于以上我们提出的概念，我们把加密过程分为两个阶段，例如阶段Ⅰ(利用帕斯卡三角进行替换)和阶段Ⅱ(利用谢尔宾斯基三角进行置换)

3.3 阶段Ⅰ：(利用帕斯卡三角替换)

在发送端，明文中的字符按照图中的三角形(三角形-1)按行排列。基于上述公式(5)和(6)，借助明文中的起始字符对其他字符进行异或操作(如三角形-2)。把这两步加在一起得到加密后的密文。阶段Ⅰ的字符替换过程如下：我们假设明文为“meet me at party”。将其按照上述方法排列而成的三角形-1如图3所示。接下来填充字符，像这种情况下以字母“x”填充到三角形的末尾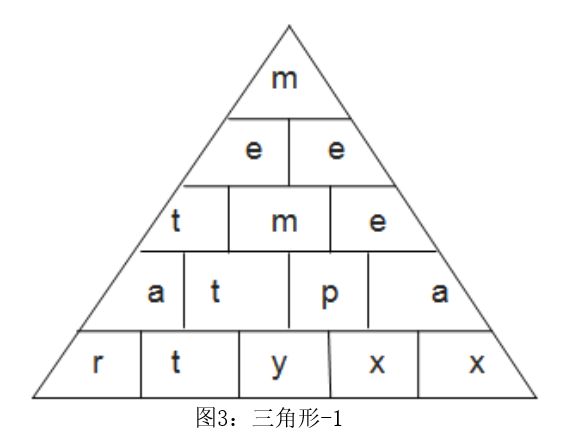利用帕斯卡三角原理替换后的三角形-2如图4所示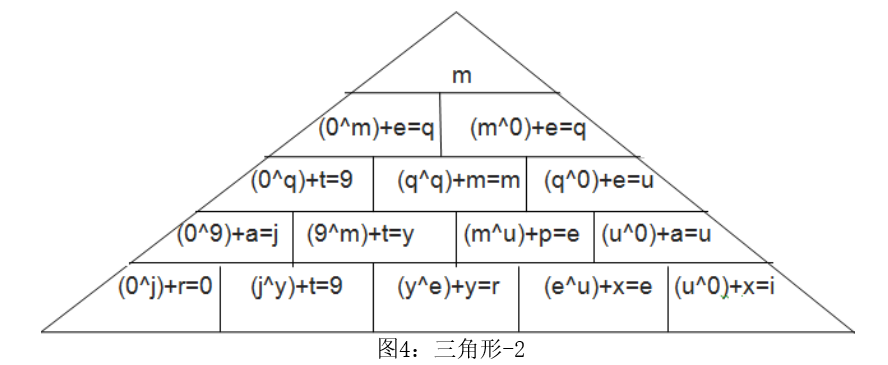：通过三角形-1和三角形-2获取到的替换后的文本如图5所示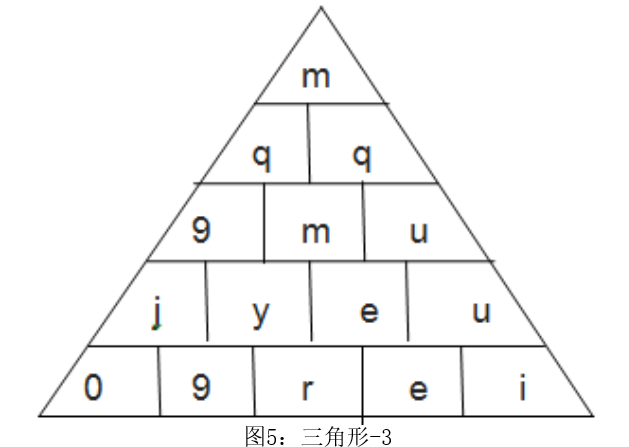：因此，在应用以上方法后我们的明文替换成了“MQQ9MUJYEU09REI”

3.4 阶段Ⅱ：(利用谢尔宾斯基三角置换)

在谢尔宾斯基三角中，我们把奇数位的字符写在前面，偶数位的字符写在后面，谢尔宾斯基三角的示例如图7所示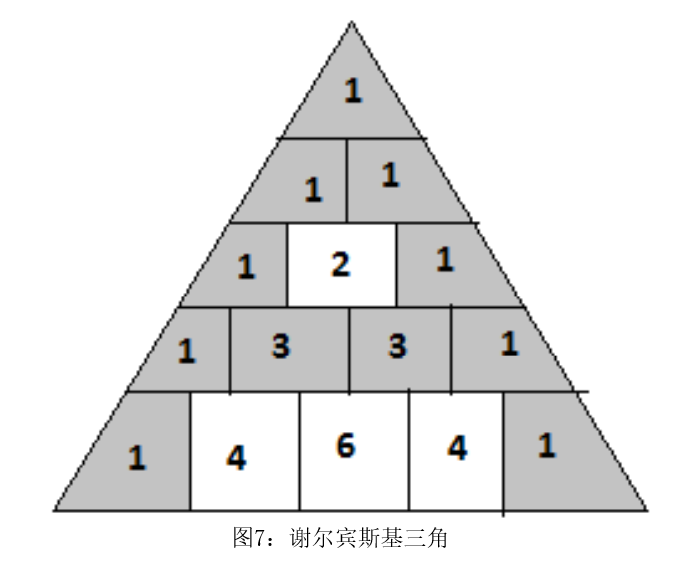把阶段Ⅰ的结果输入到阶段Ⅱ来获得最终的密文。首先把阶段Ⅰ的结果按图8所示按位排列，并根据谢尔宾斯基三角的规则读取密文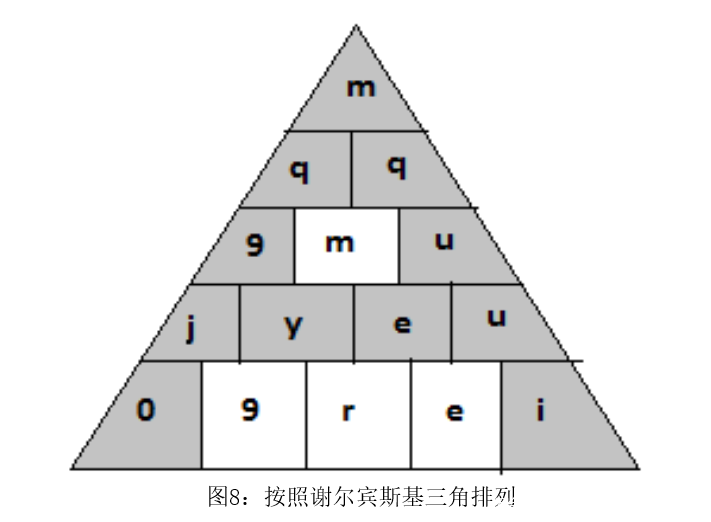因此，我们得到了由“meet me at party”加密成的密文“MQQ9UJYEU0IM9RE”

3.5 加密算法

输入：明文 输出：密文

步骤一：把明文放入一个[m,m]的矩阵中加密形成三角形-1 

 步骤二：新建一个基于帕斯卡三角规则的三角形，三角形-2，即，将处于边缘的字符和0进行异或，处于里面的字符和相邻的字符进行异或 

 步骤三：把三角形-1中的字符和三角形-2中的字符相加的结果替换原字符 

 步骤四：重复步骤三的操作直至矩阵被遍历 步骤五：按照谢尔宾斯基三角的规则读取字符 步骤六：存储密文

四、实验结果及分析

我们提出的办法是使用Java语言进行实验。系统配置是处理器为Intel i5-5200U，主频2.2GHz，RAM 4GB，Windows操作系统。使用多条不同长度的不同明文测试加密算法。基于帕斯卡三角对明文进行替换，如表1所示。按照我们提出的方法密文中重复的字符会被替换成不同的字符。计算明文与密文之间的Hamming Distance(汉明距离)以量化比特差表2给出了按照上面论述的替换和置换方法变换后的密文。明文中的字符被随机地打乱散落于密文的各个位置。计算了明文与密文之间的Hamming Distance(汉明距离)后又观察到比特差增大了在应用替换和置换变换后，我们之前所论述方法的效果得到增强。从结果来看，明文中重复的字符映射到密文中的不同字符。因此，密文不易受密码分析和字母频率攻击

五、总结

本文中，我们开发了一种使用帕斯卡和谢尔宾斯基三角形原理加解密文本信息的新密码系统。该方法非常简单且易于实现因为它涉及用替换和置换技术加密文本。明文中的字符替换成随机字符然后使用置换法将密文随机改组。所论述的加密方法明显满足混淆和扩散的特性。使用所论述方法加密后的消息不易受密码分析和字母频率攻击

参考文献

1.Acharya B, Patra S, and Panda G, “Image encryption by novel cryptosystem using matrix transformation”, Emerging Trends in Engineering and Technology出版社, 2008年. 

2.Cooper R.H, Fredericton NB, Hunter-Duvar R and Patterson W, “A more efficient public-key cryptosystem using the Pascal triangle”, World Prosperity Through Communications, IEEE International Conference(计算机与通信国际会议), 1989年,第三卷,第1165页 – 1169页. 

3.Dinesh P. Baviskar, Sidhhant N. Patil and Onkar K. Pawar, “Android based message encryption/decryption using matrix”, International Journal of Research in Engineering and Technology(国际工程技术研究期刊), 第四卷, 第一期, 2015年1月. 

4.Edwards A.W.F, “Pascal‟s Arithmetical Triangle: The Story of a Mathematical Idea”. 

5.Hazem M. El bakry, Ali E. Taki El Deen and Ahmed Hussein Ali El Tengy, “A New Mobile Application for Encrypting SMS/Multimedia Messages on Android”, International Journal of Scientific & Engineering Research(国际科学与工程研究杂志), 第四卷, 第十二期 2013年. 

6.Himani Agarwal and Monisha Sharma, “A Review of Text Encryption Techniques”, Asian Journal of Computer Science and Information Technology(亚洲计算机科学与信息技术杂志), 第四卷, 第五期, 第47页-54页, 2014年.

7.Punam V. Maitri, Rekha V. Sarawade, Mayuri P. Patil and Sarika T. Deokate, “MSC: Mobile Secure Communication Using SMS in Network Security: A Survey”, International Journal of Engineering Research & Technology(国际工程研究与技术杂志), 第二卷, 第十一期, 2013年. 

8.Rohan Rayarikar, Sanket Upadhyay and Priyanka Pimpale , “SMS Encryption using AES Algorithm on Android”, International Journal of Computer Applications(国际计算机应用杂志) (0975–8887) , 第五十卷, 第十九期, 2012年7月. 

9. Shobha Jha P U. Dutta P and Priyankgupta P , “SMS Encryption using NTRU Algorithms on Android Application”, International Journal of Scientific Engineering and Applied Science(国际科学工程与应用科学), 第二卷, 第一期, 2016年1月. 

10.Sivakumar T and Venkatesan R, “A Novel Image Encryption Approach using Matrix Reordering”, WSEAS Transactions on Computers杂志, 第十二卷, 第十一期, 2013年. 

11.Sivakumar T and Anusha T, “A New Symmetric Cryptosystem using Randomized Parameters of SHA-512 and MD5 Hash Functions”, International Journal of Innovations in Engineering and Technology(国际工程与技术创新杂志), 第六卷, 第四期, 2016年5月. 

12.Smile Markovski, Aleksandra Kuzmanovska, and Milivoj Simeonovsk, “A Protocol for Secure SMS Communication for Android OS”, ICT Innovations杂志 2011年版, 第一百五十卷, Advances in Intelligent and Soft Computing, 第171页-178页, 2011年 

13.Sri Rangarajan, Sai Ram N and Vamshi Krishna N, “Securing SMS using Cryptography”, International Journal of Computer Science and Information Technologies(国际计算机科学与信息技术期刊), 第四卷, 第二期, 第285页–288页, 2013年. 

14.Sugapriya K, Kishorekumar K and Anitha Kumari K, “A Novel Encryption Technique using Pascal Triangle for Image Cryptosystem”, National Conference on Research and Challenges in IT(全国IT研讨会议), 2016年4月22日 - 23日, PSG College of Technology, Coimbatore 

15.William Stallings, “Cryptography and Network Security-Principles and Practice”, Pearson Education出版社, 新德里, 2013年

*参考来源：academia.edu，NaTsUk0 编译整理，转载请注明来自 FreeBuf.COM。