*本文原创作者：bubbleszz，本文属FreeBuf原创奖励计划，未经许可禁止转载

前言

说起来这次的分析过程还是源于一位老哥给我分享的一份合约，写法很有意思也确实存在着很多的问题，我们等会再来谈谈它。

以太坊中数据的存储

首先我们来简单了解一下以太坊中是如何存储数据的。

对于固定大小的已知变量，EVM会直接将它们按顺序从0开始存储在每个存储位里，因为EVM虚拟机是一个256位的机器，所以它的每个存储位也都是256bit，即32个字节比如下面这个简单的合约。

pragma solidity ^0.4.23;
contract test{
    uint256 public a=6;
    uint256[2] public b;
    bytes32 c="asdwq";
    address q;
    function test(){
        q=msg.sender;
        b[0]=88;
        b[1]=99;
  }
}

我们来看看以太坊上如何存储这些变量的,这里我是在remix里通过debug页面来直接查看的，这样比较方便。

可以看到存储位即key为0的位置上存储的就是a的值，然后下面1和2的存储位上就是b的值，3号位和4号位分别是c和q，应该还是比较清楚的，所以事实上你所有的数据差不多都是在块上可见的，对于这些存储位里的数据我们可以直接通过web3.eth.getStorageAt来读取。

当然EVM中对于固定长度的变量的存储也并不就是这么简单，因为在EVM中消耗gas最多的操作就是存储操作了，不论是永久的storage还是内存的memory，当然storage又要比内存要多很多，所有solidity里进行了一定的存储优化，简单来讲，即你定义的这个变量所占的空间小于32个字节时，它所占据的这个存储位的空间可以与它后面的变量共享，当然前提是这个变量塞的下去，因为在EVM里将数据写入一个新位置和写入一个已经分配出来的位置所需的gas是不一样的，对于这部分内容就不多说了，举个简单的例子。

pragma solidity ^0.4.23;
contract test{
    uint16 public a=6;
    uint16 public b=8;
    bytes16 c="4648";
}

这里我定义的就不是256bit大小的变量了，我们再来看看它们怎么占用存储位的 。

很有意思，上面的三个变量仅占用了一个存储位，它们分别占据着空间的不同位置，实现了存储的共享。

接下来我们再来简单谈谈动态数据的存储，这包含了动态的数组和映射。

映射相对来讲简单一些,还是来看一个简单的例子。

pragma solidity ^0.4.23;
contract test{
     mapping(uint256 => uint256) z;
     function test(){
         z[233]=123;
     }
}

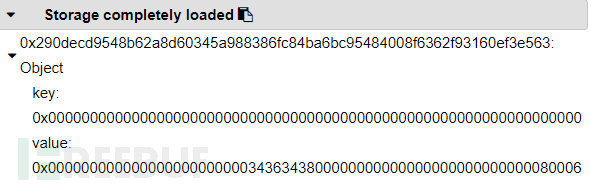
其存储如下

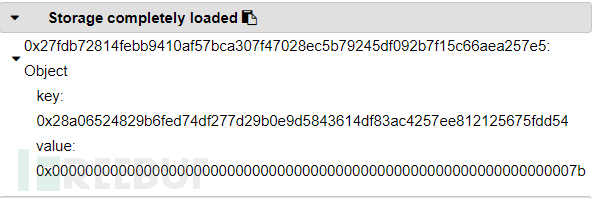这里其存储位置的计算规则就是

keccak256(bytes32(key) + bytes32(position))

此处key即为映射的key也就是233，而position也就是该变量本来的位置，这里它是定义的第一个变量，所以位置即为0，根据此式我们可以手动算出变量存储位置。

然后我们来看看动态数组的存储，这种的情况相对比较多也更为复杂，我们还是来认识一些简单的情况，毕竟这也不是今天的重点，有兴趣的可以去深入了解。

还是先来看一个简单的例子

pragma solidity ^0.4.23;
contract test{
    uint256[] public a;
    function test(){
        a.push(123);
        a.push(456);
        a.push(789);
    }
}

其存储的分布如图

我们看到其占据了四个存储位，其中position为0的位置存放的是数组的长度，下面的三个位置存放的就是数组的值，而且我们不难发现其key是依次递增的，第一个位置的计算方式也很简单，就是keccak256(position）其中的position就是存放数组长度的位置，此处即0，验证如下

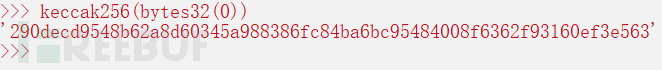然后我们再看看增加了结构体以后的存储方式。

pragma solidity ^0.4.11;
contract test {
    mapping(uint256 => gg) gg1;
    struct gg {
        uint256 a;
        uint256 b;
        uint256 c;
    }
    function test(){
        gg1[233].a=123;
        gg1[233].b=456;
        gg1[233].c=789;
    }
}

其存储结果如下

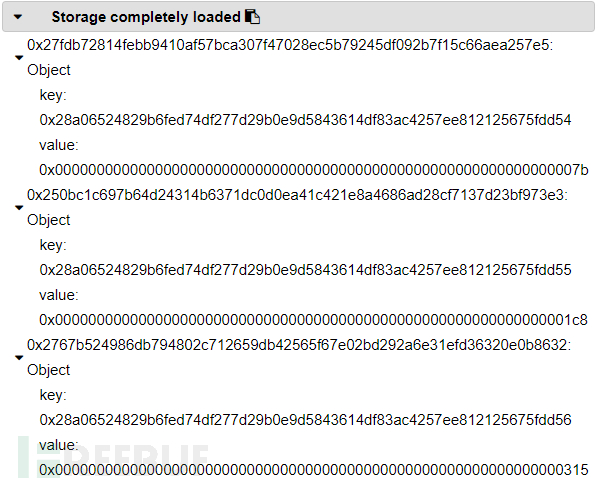跟上面的情况其实类似，首位是根据映射的计算规则得到，后面的两个存储位置在此基础上递增，应该算是比较简单了，复杂点的情况我感觉都可以拿来给ctf出题了。

一个有问题的合约

前面讲了一些基础，接下来我们开始进入正题，说起来这次分析的缘起还是下面这个合约。

pragma solidity ^0.4.24;

// To play, call the play() method with the guessed number.  Bet price: 0.1 ether

contract CryptoRoulette {

    uint256 public secretNumber;
    uint256 public lastPlayed;
    uint256 public betPrice = 0.1 ether;
    address public ownerAddr;

    struct Game {
        address player;
        uint256 number;
    }
    Game[] public gamesPlayed;

    function CryptoRoulette() public {
        ownerAddr = msg.sender;
        generateNewRandom();
    }

    function generateNewRandom() internal {
        // initialize secretNumber with a value between 0 and 15
        secretNumber = uint8(sha3(now, block.blockhash(block.number-1))) % 16;
    }

    function play(uint256 number) payable public {
        require(msg.value >= betPrice && number < 16);

        Game game;
        game.player = msg.sender;
        game.number = number;
        gamesPlayed.push(game);

        if (number == secretNumber) {
            // win!
            if(msg.value*15>this.balance){
                msg.sender.transfer(this.balance);
            }
            else{
                msg.sender.transfer(msg.value*15);
            }
        }

        generateNewRandom();
        lastPlayed = now;
    }

    function kill() public {
        if (msg.sender == ownerAddr && now > lastPlayed + 1 days) {
            suicide(msg.sender);
        }
    }

    function() public payable { }
}

乍看上去这个合约还是问题多多的，它的随机数生成算法就有很大问题，很容易就会受到攻击，将secretnumber解出来，因为攻击者想办法在调用函数的这个块里插入一次交易来窥探当前块的block.number和now即可得到secretnumber的值，这可以通过部署一个合约来调用此合约的函数来实现。

不过事实上你仔细看的话会发现该作者写的代码不仅直接将secretnumber暴露在视线里而且它的更新竟然是在将传入的值与之进行比对之后，这样的更新是完全木有任何意义的，当时还在惊奇竟然会有这样的合约存在于主链上，而且里面竟然还被存了一个eth进去。

不过当我试图在本地复现时却发现了问题，不管怎么传递number，就是没法跟secretnumber对上号，然后debug了一下才发现了端倪。

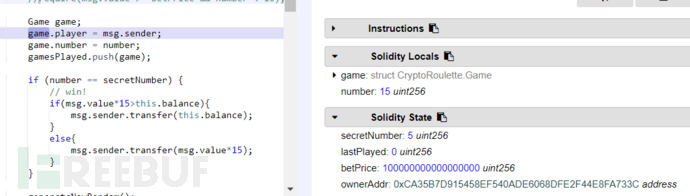
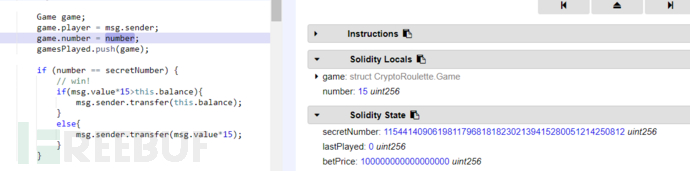从图中我们可以看到原本secretNumber的值为5，但是执行完game.player=msg.sender以后却发生了改变，变成了那一长串的数字而这串数字其实就是我们msg.sender的地址转换为int的值，然后直到下一次generatenumber执行secretNumber的值都将被这一串数字所占据，同时因为play函数的调用需要满足传入的number小于16，所以我们倒是没法利用这里的漏洞了。

不过真正让人感兴趣的还是此处结构体game的初始化对存储数据的覆盖，代码中是选择了在函数中直接初始化，而且最关键的是它没加关键字memory，memory代表的是使用内存来存储，这样可以避免占用storage的存储位，因为memory所需的gas要少得多，记得之前看到说在函数里直接初始化结构体必须加memory关键字，否则将会报错，然而这里并没有报错，只是报了warning，这就让我有点懵逼，开始怀疑是solidity的版本问题，然而我从0.4.0到0.4.24换了n多版本也没有报错。

然后我又尝试了一些结构体的初始化方式，发现当结构体被显式地初始化时才会报错，如下。

报错为Type struct test.G memory is not implicitly convertible to expected type struct test.G storage pointer。

然而结构体是并不需要这样的显式初始化也能使用的，其默认值即为存储位上的值，而此处在函数中的初始化却使用了storage存储的存储位，这就相当于一个函数内的局部变量变成了整个合约里的全局变量，因为它使用的是全局变量的存储位置，这可真是太有意思了，对于这我们再来找个更加清晰点的例子来看看。

pragma solidity ^0.4.11;

contract test {
    uint256 public a=0x123;
    uint256 public b=0x456;
    uint256 public c=0x789;
    struct G {
        uint256 a;
        uint256 b;
        uint256 c;
    }
    function testforfun(){
    G g;
    g.a=1;
    g.b=2;
    g.c=3;
    }
}

在我们执行testforfun函数前a，b，c的值都是我们部署合约时的值，但是之后便成功被函数里初始化的结构体覆盖。

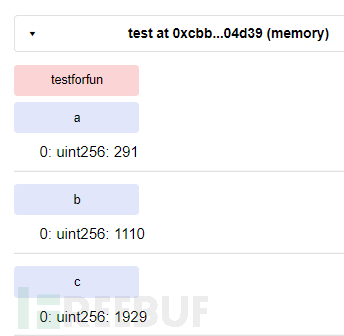
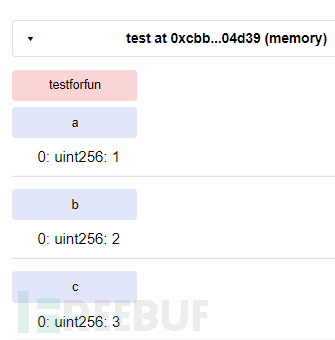感觉solidity也是比较奇葩了,同样作用的两段代码一段报错另一段却报warning，而且同样让人奇怪的就是在函数里初始化的结构体的默认的存储类型竟然就是storage，难道跟其它那些固定长度的变量一样默认使用memory存储不好么,对于这一点我们也可以直观地在汇编代码里看见。

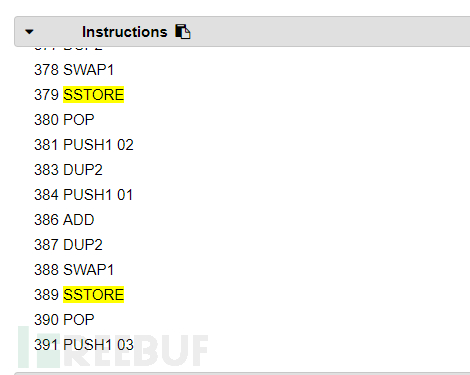调用testforfun时使用的存储代码为sstore，这就表示其中的结构体使用的是storage，而对应地使用memory关键字以后或者那些默认即为memory存储的变量使用的存储代码为mstore。

然后我便想看看其它类型的变量是否也会存在类似的情况，然后便发现了更有意思的数组类型，不管是固定长度的数组函数动态的数组，在函数内定义时没有加上memory关键字的话都会默认使用storage存储，去占领全局变量的空间。

例如一个简单的定长数组

pragma solidity ^0.4.11;

contract test {
    uint256 public a=0x123;
    uint256 public b=0x456;
    uint256 public c=0x789;

    function testforfun(){
    uint256[3] z;
    z[0]=1;
    z[1]=2;
    z[2]=3;
    }
}

得到的结果如下

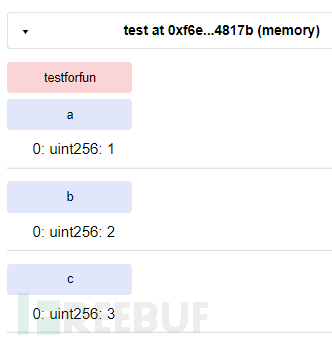依然是很直接的覆盖，同样的，对于动态的数组情况也是类似

pragma solidity ^0.4.11;

contract test {
    uint256[] public a;
    function test(){
        a.push(123);
        a.push(456);
    }
    function testforfun(){
    uint256[] z;
    z[0]=1;
    z[1]=2;
    }
}

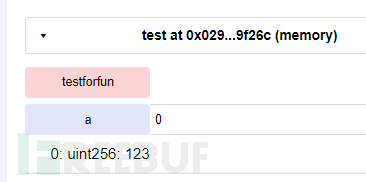
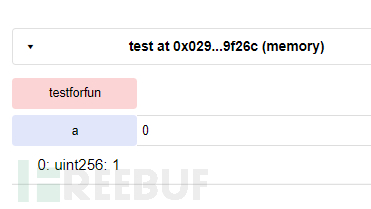这里动态数组的存储形式我们之前也提到了，利用函数定义内的动态数组可以覆盖合约里相同位置上动态数组的数据，确实是相当有意思了。

到这里我们不妨再回到前面那个合约，现在我们知道了事实上合约内的secretNumber和lastPlayed都会被初始化的game结构体覆盖，如果不是play函数的入口处有限制的话就完了，我倒是有点怀疑是不是作者故意这么写的，这就很骚了，毕竟没人能成功答对secretNumber的值，哪怕你把play函数中调用generatenumber的位置放在最前面，这样看上去只有一个随机数可被预测的漏洞，然而想要成功破解也是徒劳。

写在最后

通过这一次的分析过程也让我对以太坊的数据存储有了更深的理解，可以看到它跟其它的编程语言还是有着很大的区别的，如果不了解EVM的运行机制，一个初来乍到的程序员很容易就会犯错，写出存在漏洞的代码，毕竟这很多也是其它编程语言里带过来的习惯，当然我感觉这次的这种漏洞的锅还得solidity来背，感觉明明这种情况应该是需要报错的，结果却只是弹了warning，这样不排除有些开发者可能完全不考虑gas的高消耗的情况下来滥用storage存储，而且我感觉solidity里对函数中初始化的默认存储形式也该改改。

不得不说这种变量覆盖的形式还是挺有意思的，其实前面提到的各种可能的覆盖形式通过各种组合感觉会有很多种神奇的效果，这就留给大家自己去探索了。

*本文原创作者：bubbleszz，本文属FreeBuf原创奖励计划，未经许可禁止转载